题目内容
9.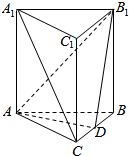 如图,已知在直三棱柱ABC-A1B1C1中,AB=AA1=2,∠ACB=$\frac{π}{3}$,点D是线段BC的中点.
如图,已知在直三棱柱ABC-A1B1C1中,AB=AA1=2,∠ACB=$\frac{π}{3}$,点D是线段BC的中点.(Ⅰ)求证:A1C∥平面AB1D;
(Ⅱ)当三棱柱ABC-A1B1C1的体积最大时,求直线A1D与平面AB1D所成角θ的正弦值.
分析 (Ⅰ)要证A1C∥平面AB1D,可利用线面平行的判定,记A1B∩AB1=O,由点D是线段BC的中点,可得A1C∥OD,然后由线面平行的判定定理得答案;
(Ⅱ)法一、由题意可得当三棱柱ABC-A1B1C1的底面积最大时,体积最大,进一步可得此时三角形ABC为正三角形,然后利用等积法求出点A1到平面AB1D的距离d,由sinθ=$\frac{d}{D{A}_{1}}$得答案.
法二、以D为原点,直线DA,DC分别为x,y轴建立空间坐标系,求出平面AB1D的一个法向量,进一步求出|cos<$\overrightarrow{D{A}_{1}},\overrightarrow{n}$>|得到直线A1D与平面AB1D所成角θ的正弦值.
解答 (Ⅰ)证明:记A1B∩AB1=O,OD为三角形A1BC的中位线,
∵A1C∥OD,OD?平面A1BD,A1C?平面AB1D
∴A1C∥平面AB1D;
(Ⅱ)解:法一、当三棱柱ABC-A1B1C1的底面积最大时,体积最大,
$4=A{B}^{2}=A{C}^{2}+B{C}^{2}-2•AC•BC•cos\frac{π}{3}$≥2AC•BC-AC•BC=AC•BC,
当AC=BC,即三角形ABC为正三角形时取最大值.
设点A1到平面AB1D的距离为d,由${V}_{{A}_{1}-A{B}_{1}D}={V}_{C-A{B}_{1}D}={V}_{{B}_{1}-ACD}$,得
$\frac{1}{3}{S}_{△A{B}_{1}D}•d=\frac{1}{6}AD•D{B}_{1}•d=\frac{\sqrt{3}}{3}$,∴$d=\frac{2\sqrt{5}}{5}$.
则sinθ=$\frac{d}{{A}_{1}D}=\frac{\frac{2\sqrt{5}}{5}}{\sqrt{7}}=\frac{2\sqrt{35}}{35}$.
法二、如图,
以D为原点,直线DA,DC分别为x,y轴建立空间坐标系,
则A($\sqrt{3},0,0$),B(0,-1,0),B1(0,-1,2),${A}_{1}(\sqrt{3},0,2)$.
设面AB1D的法向量为$\overrightarrow{n}=(x,y,z)$,
由$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{DA}=\sqrt{3}x=0}\\{\overrightarrow{n}•\overrightarrow{D{B}_{1}}=-y+2z=0}\end{array}\right.$,
设y=2,则z=1,∴$\overrightarrow{n}=(0,2,1)$,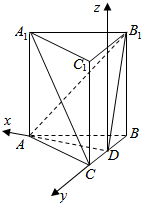
又$\overrightarrow{D{A}_{1}}=(\sqrt{3},0,2)$,
∴sinθ=|cos<$\overrightarrow{D{A}_{1}},\overrightarrow{n}$>|=$\frac{|\overrightarrow{D{A}_{1}}•\overrightarrow{n}|}{|\overrightarrow{D{A}_{1}}|•|\overrightarrow{n}|}$=$\frac{2\sqrt{35}}{35}$.
点评 本题考查直线与平面平行的判定,考查直线与平面所成的角,训练了利用向量法求线面角,考查学生的空间想象能力和运算能力,是中档题.

 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案| A. | $\frac{lnx+1}{{x}^{2}}$ | B. | $\frac{lnx-1}{{x}^{2}}$ | C. | $\frac{x+lnx}{{x}^{2}}$ | D. | $\frac{1-lnx}{{x}^{2}}$ |
| A. | 第5项 | B. | 第6项 | C. | 第7项 | D. | 第5项或第6项 |
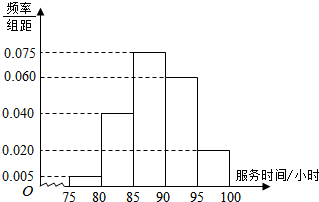 某市规定,高中学生三年在校期间参加不少于80小时的社区服务才合格.教育部门在全市随机抽取200位学生参加社区服务的数据,按时间段[75,80),[80,85),[85,90),[90,95),[95,100](单位:小时)进行统计,其频率分布直方图如图所示.
某市规定,高中学生三年在校期间参加不少于80小时的社区服务才合格.教育部门在全市随机抽取200位学生参加社区服务的数据,按时间段[75,80),[80,85),[85,90),[90,95),[95,100](单位:小时)进行统计,其频率分布直方图如图所示.