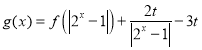Question

【题目】某港口的水深（米）是时间（，单位：小时）的函数，下面是每天时间与水深的关系表：

	0	3	6	9	12	15	18	21	24
	10	13	9.9	7	10	13	10.1	7	10

经过长期观测， 可近似的看成是函数

（1）根据以上数据，求出的解析式

（2）若船舶航行时，水深至少要11.5米才是安全的，那么船舶在一天中几个小时可以安全的进出该港？

Answer 1

【答案】（1） ；（2）8个小时

【解析】

（1）观察数据可知水深最大值为13，最小值为7，列式求，再根据12小时达到依次最大值说明周期为12，求出即可；（2），即，再解关于的三角不等式即可求出船舶在一天中的哪几段事件可以安全的进出该港.

（1）由表中数据可以看到：水深最大值为13，最小值为7，

所以 ，，

且相隔9小时达到一次最大值说明周期为12，因此，，

故

（2）要想船舶安全，必须深度，即

∴ 解得：

又

当时，；当时，；

故船舶安全进港的时间段为，，共8个小时.