题目内容
【题目】（本小题满分12分）
某工厂生产甲、乙两种产品，已知生产每吨甲、乙两种产品所需煤、电力、劳动力、获得利润及每天资源限额（最大供应量）如表所示：
| 甲产品 | 乙产品 | 资源限额 |
煤（t） | 9 | 4 | 360 |
电力（kw·h） | 4 | 5 | 200 |
劳力（个） | 3 | 10 | 300 |
利润（万元） | 7 | 12 |
问：每天生产甲、乙两种产品各多少吨，获得利润总额最大？
【答案】每天生产甲２０吨、乙２４吨，获得利润总额最大
【解析】试题分析：解：设此工厂应分别生产甲、乙两种产品x吨、y吨，获得利润z万元 （1分）
依题意可得约束条件：
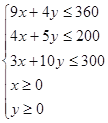……（4分） （2分）
利润目标函数
（7分）
如图，作出可行域，作直线
，把直线l向右上方平移至l1位置，直线经过可行域上的点M，且与原点距离最大，此时取最大值. （10分）
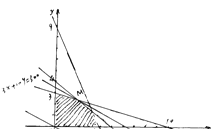
解方程组
，得M（20，24）
故，生产甲种产品20t，乙种产品24 t，才能使此工厂获得最大利润. （12分）
练习册系列答案
相关题目
【题目】下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量（
吨）与相应的生产能耗
（吨）标准煤的几组对照数据：
| 1 | 2 | 3 | 4 | 5 |
| 2 | 3 | 6 | 9 | 10 |
（1）请画出上表数据的散点图；
（2）请根据上表提供的数据，用最小二乘法求出关于的线性回归方程
；
（3）已知该厂技术改造前100吨甲产品能耗为200吨标准煤，试根据（2）求出的线性回归方程，预测生产100吨甲产品的生产能耗比技术改造前降低多少吨标准煤？
