Question

【题目】已知函数f（x）=ex（e=2.71828…），g（x）为其反函数．
（1）求函数F（x）=g（x）﹣ax的单调区间；
（2）设直线l与f（x），g（x）均相切，切点分别为（x1 ， f（x1）），（x2 ， f（x2）），且x1＞x2＞0，求证：x1＞1．

Answer 1

【答案】
（1）解：∵f（x）=ex，g（x）为其反函数，故g（x）=lnx，（x＞0），

∴F（x）=g（x）﹣ax=lnx﹣ax，g′（x）= ，

①a≤0时，F′（x）＞0，F（x）在（0，+∞）递增，

②a＞0时，令F′（x）＞0，解得：x＜ ，令F′（x）＜0，解得：x＞ ，

故F（x）在（0， ）递增，在（ ，+∞）递减

（2）解：f′（x）=ex，g′（x）= ，

切点的坐标分别为（x1，ex1），（x2，lnx2），可得方程组：

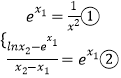，∵x1＞x2＞0，

∴ex1＞1，∴ =ex1＞1，

∴0＜x2＜1．

由②得lnx2﹣ex1=ex1（x2﹣x1），

∴lnx2=ex1（x2﹣x1+1）．

∵0＜x2＜1，∴lnx2＜0，

∴x2﹣x1+1＜0，即x1＞x2+1＞1．

∴x1＞1．

【解析】（1）求出F（x）的导数，通过讨论a的范围，解关于导函数的不等式，求出函数的单调区间即可；（2）由于直线l与f（x）、g（x）均相切，利用导数的几何意义和斜率计算公式可得方程组，再利用x1＞x2＞0，可得ex1＞1，得到0＜x2＜1．再利用②得lnx2=ex1（x2﹣x1+1）＜0，即可得到x2﹣x1+1＜0．
【考点精析】本题主要考查了利用导数研究函数的单调性的相关知识点，需要掌握一般的,函数的单调性与其导数的正负有如下关系： 在某个区间内，(1)如果，那么函数在这个区间单调递增；(2)如果，那么函数在这个区间单调递减才能正确解答此题．