题目内容
【题目】如图,在三陵锥![]() 中,
中,![]() 为等腰直角三角形,
为等腰直角三角形,![]() ,
,![]() 为正三角形,
为正三角形,![]() 为
为![]() 的中点.
的中点.
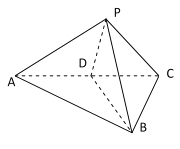
(1)证明:平面![]() 平面
平面![]() ;
;
(2)若二面角![]() 的平面角为锐角,且棱锥
的平面角为锐角,且棱锥![]() 的体积为
的体积为![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)根据等腰三角形三线合一,可证明线线垂直,再根据线面垂直判定定理,即可证明;
(2)根据题意,点![]() 在平面
在平面![]() 内的射影
内的射影![]() 在射线
在射线![]() 上,再根据锥体体积公式可知
上,再根据锥体体积公式可知![]() ,由线面垂直的判定定理,可证
,由线面垂直的判定定理,可证![]() 平面
平面![]() ,则建系:以
,则建系:以![]() 为坐标原点,
为坐标原点,![]() 所在直线分别为
所在直线分别为![]() 轴,
轴,![]() 轴,
轴,![]() 轴建立空间直角坐标系,利用空间向量法,求线面角.
轴建立空间直角坐标系,利用空间向量法,求线面角.
(1)
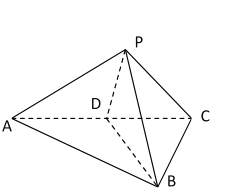
证明:∵![]() ,
,![]() 为
为![]() 中点,∴
中点,∴![]() ,
,
又![]() 为等边三角形,
为等边三角形,![]() ,∴
,∴![]() ,
,
![]() ,∴
,∴![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,∴平面
,∴平面![]() 平面
平面![]() ;
;
(2)由(1)知点![]() 在平面
在平面![]() 内的射影
内的射影![]() 在直线
在直线![]() 上,又二面角
上,又二面角![]() 的平面角为锐角,∴
的平面角为锐角,∴![]() 在射线
在射线![]() 上,
上,![]() ,
,![]() ,∴
,∴![]() ,
,
又![]() ,∴
,∴![]() ,即
,即![]() 为
为![]() 中点,取
中点,取![]() 中点
中点![]() ,连接
,连接![]() ,则
,则![]() ,
,
∴![]() 平面
平面![]() ,∴
,∴![]() 两两互相垂直,
两两互相垂直,
以![]() 为坐标原点,
为坐标原点,![]() 所在直线分别为
所在直线分别为![]() 轴,
轴,![]() 轴,
轴,![]() 轴建立空间直角坐标系,
轴建立空间直角坐标系,
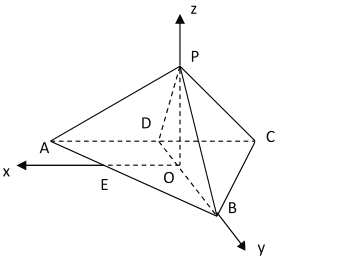
则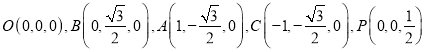
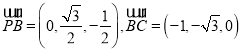
设平面![]() 的法向量为
的法向量为![]()
由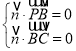 得
得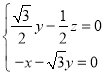
令![]() ,得平面
,得平面![]() 的一个法向量为
的一个法向量为![]() ,
,
又 ,设
,设![]() 与平面
与平面![]() 所成角为
所成角为![]() ,
,
则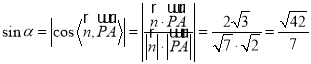 ,
,
∴直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案【题目】对于很多人来说,提前消费的认识首先是源于信用卡,在那个工资不高的年代,信用卡绝对是神器,稍微大件的东西都是可以选择用信用卡来买,甚至于分期买,然后慢慢还!现在银行贷款也是很风靡的,从房贷到车贷到一般的现金贷.信用卡“忽如一夜春风来”,遍布了各大小城市的大街小巷.为了解信用卡在![]() 市的使用情况,某调查机构借助网络进行了问卷调查,并从参与调查的网友中随机抽取了100人进行抽样分析,得到如下
市的使用情况,某调查机构借助网络进行了问卷调查,并从参与调查的网友中随机抽取了100人进行抽样分析,得到如下![]() 列联表(单位:人)
列联表(单位:人)
经常使用信用卡 | 偶尔或不用信用卡 | 合计 | |
40岁及以下 | 15 | 35 | 50 |
40岁以上 | 20 | 30 | 50 |
合计 | 35 | 65 | 100 |
(1)根据以上数据,能否在犯错误的概率不超过0.10的前提下认为![]() 市使用信用卡情况与年龄有关?
市使用信用卡情况与年龄有关?
(2)①现从所抽取的40岁及以下的网民中,按“经常使用”与“偶尔或不用”这两种类型进行分层抽样抽取10人,然后,再从这10人中随机选出4人赠送积分,求选出的4人中至少有3人偶尔或不用信用卡的概率;
②将频率视为概率,从![]() 市所有参与调查的40岁以上的网民中随机抽取3人赠送礼品,记其中经常使用信用卡的人数为
市所有参与调查的40岁以上的网民中随机抽取3人赠送礼品,记其中经常使用信用卡的人数为![]() ,求随机变量
,求随机变量![]() 的分布列、数学期望和方差.
的分布列、数学期望和方差.
参考公式: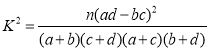 ,其中
,其中![]() .
.
参考数据:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |