Question

【题目】已知函数.

（1）若关于的方程有且只有一个实数根，求实数的取值范围；

（2）若函数的图象总在函数图象的下方，求实数的取值范围.

Answer 1

【答案】（1）；（2）.

【解析】

（1）由得出，可得出，令，将问题转化为直线与函数的图象只有一个交点，利用导数分析函数的单调性和极值，利用数形结合思想可求得实数的取值范围；

（2）由题意可知不等式对任意的恒成立，令，对实数进行分类讨论，分析函数在区间上的单调性，结合可求得实数的取值范围.

（1）令，得，

设，则直线与函数的图象只有一个交点，

函数的定义域为，，

令，得，列表如下：

		极大值

所以，函数在处取得极大值，即，如下图所示：

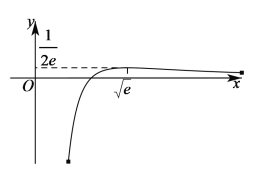
由上图可知，当或时，即当或时，直线与函数的图象只有一个交点，

因此，实数的取值范围是；

（2）令，根据题意知，当时，恒成立.

又.

①若，对任意的恒成立，此时，函数在区间上单调递减，

所以，，得，此时；

②若，当时，；当时，.

所以，函数在区间上单调递减，在区间上单调递增.

当时，，不合乎题意；

③若，对任意的，，则函数在区间上单调递增.

当时，，不合乎题意.

综上，所求实数的取值范围是.