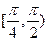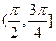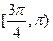题目内容
(本题满分14分)
已知函数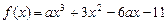 ,
,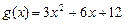 ,和直线
,和直线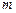 :
: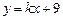 .
.
又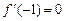 .
.
(1)求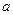 的值;
的值;
(2)是否存在 的值,使直线
的值,使直线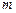 既是曲线
既是曲线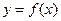 的切线,又是
的切线,又是 的切线;如果存在,求出k的值;如果不存在,说明理由.
的切线;如果存在,求出k的值;如果不存在,说明理由.
(3)如果对于所有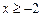 的
的 ,都有
,都有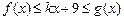 成立,求k的取值范围.
成立,求k的取值范围.
已知函数
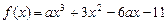 ,
,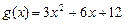 ,和直线
,和直线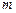 :
: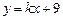 .
.又
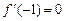 .
. (1)求
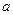 的值;
的值;(2)是否存在
 的值,使直线
的值,使直线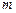 既是曲线
既是曲线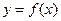 的切线,又是
的切线,又是 的切线;如果存在,求出k的值;如果不存在,说明理由.
的切线;如果存在,求出k的值;如果不存在,说明理由.(3)如果对于所有
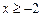 的
的 ,都有
,都有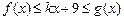 成立,求k的取值范围.
成立,求k的取值范围.(1)
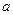 =-2.
=-2.(2)
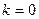
(3)

解:(1) ,因为
,因为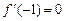 所以
所以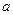 =-2. …………2分
=-2. …………2分
(2)因为直线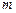 恒过点(0,9).先求直线
恒过点(0,9).先求直线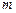 是
是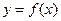 的切线.
的切线.
设切点为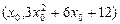 , …………3分
, …………3分
∵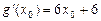 .∴切线方程为
.∴切线方程为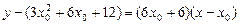 ,
,
将点(0,9)代入得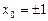 .
.
当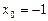 时,切线方程为
时,切线方程为 ="9," 当
="9," 当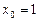 时,切线方程为
时,切线方程为 =
=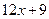 .
.
由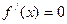 得
得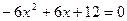 ,即有
,即有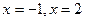
当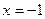 时,
时,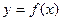 的切线
的切线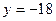 ,
,
当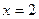 时,
时, 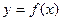 的切线方程为
的切线方程为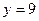 …………6分
…………6分
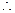
 是公切线,又由
是公切线,又由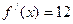 得
得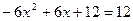
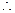
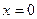 或
或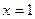 ,
,
当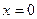 时
时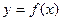 的切线为
的切线为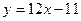 ,当
,当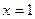 时
时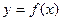 的切线为
的切线为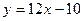 ,
,
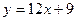 ,不是公切线, 综上所述
,不是公切线, 综上所述 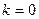 时
时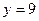 是两曲线的公切线 ……7分
是两曲线的公切线 ……7分
(3).(1)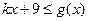 得
得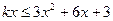 ,当
,当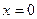 ,不等式恒成立,
,不等式恒成立,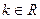 .
.
当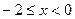 时,不等式为
时,不等式为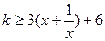 ,……8分
,……8分
而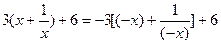
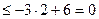
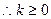
当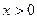 时,不等式为
时,不等式为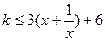 ,
,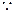
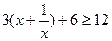
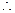
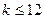
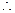 当
当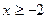 时,
时,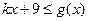 恒成立,则
恒成立,则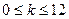 …………10分
…………10分
(2)由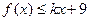 得
得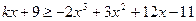
当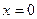 时,
时,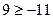 恒成立,
恒成立,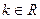 ,当
,当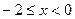 时有
时有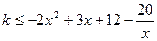
设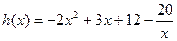 =
=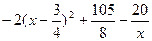 ,
,
当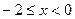 时
时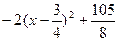 为增函数,
为增函数,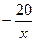 也为增函数
也为增函数
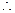
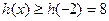
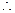 要使
要使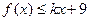 在
在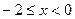 上恒成立,则
上恒成立,则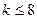 …………12分
…………12分
由上述过程只要考虑 ,则当
,则当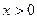 时
时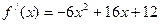 =
=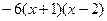
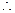 在
在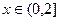 时
时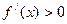 ,在
,在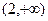 时
时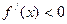
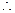
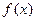 在
在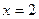 时有极大值即
时有极大值即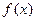 在
在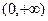 上的最大值,…………13分
上的最大值,…………13分
又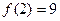 ,即
,即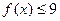 而当
而当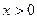 ,
,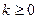 时
时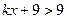 ,
,
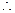
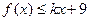 一定成立,综上所述
一定成立,综上所述 . …………14分
. …………14分
 ,因为
,因为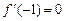 所以
所以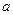 =-2. …………2分
=-2. …………2分(2)因为直线
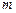 恒过点(0,9).先求直线
恒过点(0,9).先求直线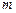 是
是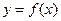 的切线.
的切线.设切点为
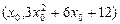 , …………3分
, …………3分∵
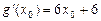 .∴切线方程为
.∴切线方程为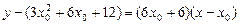 ,
,将点(0,9)代入得
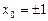 .
.当
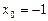 时,切线方程为
时,切线方程为 ="9," 当
="9," 当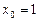 时,切线方程为
时,切线方程为 =
=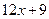 .
.由
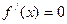 得
得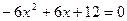 ,即有
,即有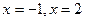
当
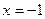 时,
时,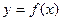 的切线
的切线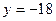 ,
,当
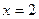 时,
时, 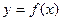 的切线方程为
的切线方程为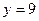 …………6分
…………6分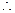
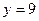 是公切线,又由
是公切线,又由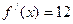 得
得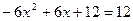
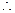
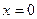 或
或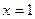 ,
,当
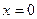 时
时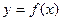 的切线为
的切线为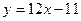 ,当
,当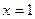 时
时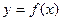 的切线为
的切线为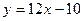 ,
,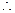
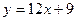 ,不是公切线, 综上所述
,不是公切线, 综上所述 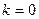 时
时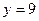 是两曲线的公切线 ……7分
是两曲线的公切线 ……7分(3).(1)
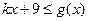 得
得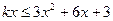 ,当
,当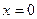 ,不等式恒成立,
,不等式恒成立,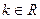 .
.当
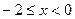 时,不等式为
时,不等式为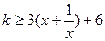 ,……8分
,……8分而
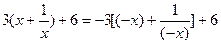
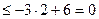
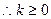
当
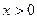 时,不等式为
时,不等式为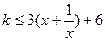 ,
,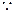
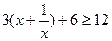
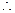
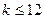
 当
当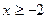 时,
时,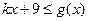 恒成立,则
恒成立,则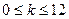 …………10分
…………10分(2)由
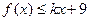 得
得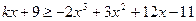
当
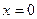 时,
时,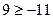 恒成立,
恒成立,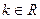 ,当
,当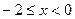 时有
时有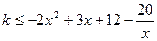
设
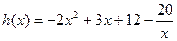 =
=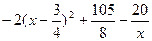 ,
,当
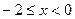 时
时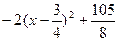 为增函数,
为增函数,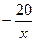 也为增函数
也为增函数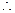
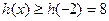
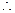 要使
要使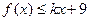 在
在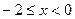 上恒成立,则
上恒成立,则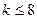 …………12分
…………12分由上述过程只要考虑
 ,则当
,则当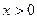 时
时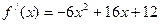 =
=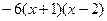
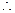 在
在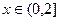 时
时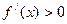 ,在
,在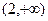 时
时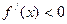
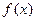 在
在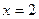 时有极大值即
时有极大值即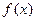 在
在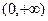 上的最大值,…………13分
上的最大值,…………13分又
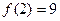 ,即
,即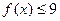 而当
而当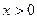 ,
,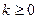 时
时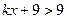 ,
,
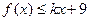 一定成立,综上所述
一定成立,综上所述 . …………14分
. …………14分
练习册系列答案
相关题目
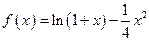 ;
;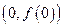 处的切线方程;
处的切线方程;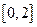 上的最大值和最小值.
上的最大值和最小值.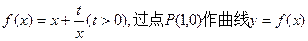 的两条切线PM、PN,切点分别为M、N.
的两条切线PM、PN,切点分别为M、N.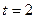 时,求函数
时,求函数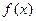 的单调递增区间;
的单调递增区间;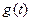 ,试求函数
,试求函数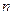 ,在区间
,在区间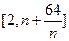 内总存在
内总存在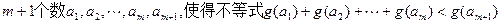 成立,求m的最大值.
成立,求m的最大值.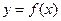 的对称轴为
的对称轴为 ,当
,当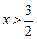 时
时 , 则
, 则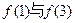 的大小关系为( )
的大小关系为( )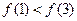
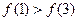
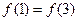

 ,则曲线在点
,则曲线在点 处的切线方程为
处的切线方程为



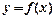 的图象在点P处的切线方程是
的图象在点P处的切线方程是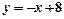 ,则
,则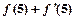 =
=  .
.  在点(-1,-3)处的切线方程是( )
在点(-1,-3)处的切线方程是( )



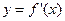 是函数
是函数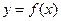 的导函数,且函数
的导函数,且函数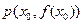 处的切线为
处的切线为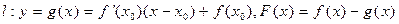 ,如果函数
,如果函数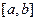 上的图像如图所示,且
上的图像如图所示,且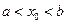 ,那么 ( )
,那么 ( )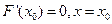 是
是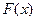 的极大值
的极大值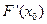 =
=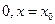 是
是 不是
不是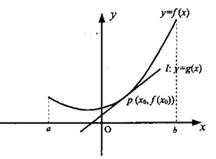
 在曲线
在曲线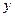 =
=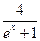 上,
上,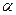 为曲线在点
为曲线在点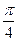 )
)