äãá¢áÖàï
Àƒäãá¢À¢á°ÅÈöˆêùä§ù¼Ø£øøÅôçá§äîÏáÈò§È˜§½ÅÅêùØ£üŸ¢öäãòçîÕȘ¥æ¯ÁöˆòçîÕ¯ÁȘØدÁöˆÑåÝà¯ÁȘ¥æØØꧯÁçáàùò»ƒªöˆ50àùȘأáõ¤µÑåꧯÁ§½ÅÅýãòåȘýãòå°è¥´çáñøæÕú½¥ðöˆ[80Ș90ÈˋÀÂ[90Ș100ÈˋÀÂ[100Ș110ÈˋÀÂ[110Ș120ÈˋÀÂ[120Ș130ÈˋȘÆèÇùçûç§ê§¡—¯Áýãòå°è¥´çáóçôòñøý¥øÝñ§ë¥È¤ 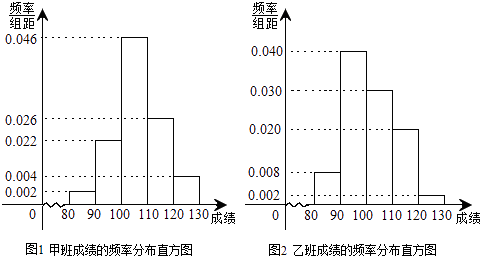
È´1Èˋëõ°èüôûÌ2Àê2êÅêˆÝÚȘáÐáÉÆÅ97.5%çá¯îöíàüöˆÀ¯íãꧡ—¯ÁåÖíãÇöýãòåøŰ襴çáýŸØšÆŠòçòˋ¢öäãòçîÕÆÅ¿ÄÀÝôÞÈ¢ýÂùçû¼âÚÆèÈ£
°è¥´ÅÀÆÖ100ñø | °è¥´ý£ÅÀÆÖ100ñø | ¤ü¥ó | |
¥æ¯Á | a= | b= | 50 |
ØدÁ | c=24 | d=26 | 50 |
¤ü¥ó | e= | f= | 100 |
È´2ÈˋüøÇÆØدÁ50àùøÅàöØã°ÕàÀ3àùȘ¥úÎöÝÚòƒ°Õç§ýãòå°è¥´åÖ[100Ș120Èˋçáàùò»È˜úµÎöçáñøý¥êŤëò»îÏóÖë«EÎöÈÛ
¡§È¤K2= ![]() ȘóðøÅn=a+b+c+d
ȘóðøÅn=a+b+c+d
PÈ´K2Àïk0Èˋ | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 2.072 | 2.706 | 3.841 | 5.204 | 6.635 | 7.879 | 10.828 |
ÀƒÇÞ¯¡À¢
È´1Èˋ12È£38È£36È£64
È´2Èˋ§ãȤØدÁýãòå°è¥´åÖ[100Ș120ÈˋçáÆÅ25àùȘÎö¢èàÀ0Ș1Ș2Ș3Ș
PÈ´Îö=0Èˋ= ![]() =
= ![]() ȘPÈ´Îö=1Èˋ=
ȘPÈ´Îö=1Èˋ= ![]() =
= ![]()
PÈ´Îö=2Èˋ= ![]() =
= ![]() ȘPÈ´Îö=3Èˋ=
ȘPÈ´Îö=3Èˋ= ![]() =
= ![]()
Îöçáñøý¥êÅòú
Îö | 0 | 1 | 2 | 3 |
P |
|
|
|
|
EÎö=0Àê ![]() +1Àê
+1Àê ![]() +2Àê
+2Àê ![]() +3Àê
+3Àê ![]() =
= ![]()
Àƒ§ãö—À¢È´1ÈˋÆèäãØãȘa=0.024Àê10Àê50=12Șb=50ˋ12=38Șe=12+24=36Șf=38+26=64Ș
ÀÁ ![]() Ș
Ș
ÀÔPÈ´K2ȃ5.204Èˋ=0.025Ș
ÀÁÆÅ97.5%çá¯îöíàüöˆíãꧡ—¯ÁåÖíãÇöýãòåøŰ襴çáýŸØšÆŠòçòˋ¢öäãòçîÕÆÅ¿ÄÀÝ
Àƒ¢¥çЃ¨ö—À¢§ãÇÞÇùäãçá¿Ä¥■åÖÆÖâÚ§ãóçôòñøý¥øÝñ§ë¥çáüÁ¿ÄøˆòÑȘíóöíóçôòñøý¥ÝÚ¤ëóçôòñøý¥øÝñ§ë¥È˜òúÑåüÁë˜ò»ƒïçáê§øøý£ë˜ÝÚÇÿñ§ò§.Æû§¶ÇíçáÝÚ¡þ¡áÝðò»ƒïçáééêÅñ§ò§¤ë¿¿°èÅöò§È˜¢èí¿òƒò»ƒïçáñøý¥úÕ¢—.ë´¿»æ¼ë¥¥à¢èØåÇÆò»ƒïøÅäÃàÀÅéüÂȘÆø¢èØåâ«Æûë¥ÅöǨçïÅéüÂȘØ奯ÑåÆûîªÝƒçáóçôòñøý¥¿â¥óæÉäÍñøý¥çáâÚ§ãȘêù§ãîªÝƒò»ƒïçáóçôòñøý¥ÝÚ¤ëóçôòñøý¥øÝñ§ë¥È˜òúë´¿»¡¼ÅÀæÕò»ƒïåÖîªÝƒàïê¢øÅùªí¥Ýàâ»ÇµÅÀâÇÝÚòƒò»ƒïçáñøý¥¿ÌôèȘù■¢èØåàûöØûú¡■úÍ°±çá¢Çç§í«¡—îªÝƒò»ƒïçáóçôòñøý¥úÕ¢—ȘýÂÆèÇù¿â¥óæÉäÍçáñøý¥úÕ¢—ÈÛ

Àƒäãá¢À¢¥¡¡—åôú¯È˜°èÑ¥§øëñ¢ˆò¥ÅùóÞÀ¯mobikeÀÝÀÂÀ¯ofoÀÝçà¿ýüÚçË°çȘíãîªçá¿ýüÚçË°çöˆ¤ÉÑÁòÅûþ§ãƒ—êù柤µØ£¿¨âÿçá°—ÅÅáîäãÈÛà£Ñ½È˜íãøøáÈò§ØýÆ—ç§êùØ£ÅˋàûàùßüßöçáöòäãȘÝààÓôØëÈôØñéȘ£·§¨¿ýüÚçË°çí¥öˆÀ¯ù§ÆÅÀÝçàÈÛ
öˆÇùȘᰣº¿¿ƒëòúñþøÏ°øñÂí¿¿ýüÚçË°çùÌ£ºç¼ýÕêù50àùȘù«ûúáõêðçáñøý¥¥¯øÏ°øñÂí¿¿ýüÚçË°ççáàùò»ë°¥óàÓüôÝÚȤ
áõêð |
|
|
|
|
|
|
òÉñûàùò» | 5 | 6 | 15 | 9 | 10 | 5 |
øÏ°øñÂí¿ ¿ýüÚçË°çàùò» | 4 | 5 | 12 | 9 | 7 | 3 |
È´ÂþÈˋÆèØåèüë°¥óò»ƒïäŸÅÇüôûÌçá![]() êÅêˆÝÚȘýÂéÅÑüáÉñþåÖñ¡ÇÚöµçá¡éôòý£°˜¿»0.1çáú¯äÃüôȘàüöˆáõêðÆŠòúñþøÏ°øñÂí¿¿ýüÚçË°çÆÅ¿ÄüçÈ£
êÅêˆÝÚȘýÂéÅÑüáÉñþåÖñ¡ÇÚöµçá¡éôòý£°˜¿»0.1çáú¯äÃüôȘàüöˆáõêðÆŠòúñþøÏ°øñÂí¿¿ýüÚçË°çÆÅ¿ÄüçÈ£
áõêðçëÆÖ35ùõ | áõêðý£çëÆÖ35ùõ | ¤ü¥ó | |
øÏ°ø | |||
ý£øÏ°ø | |||
¤ü¥ó |
ȴ·Èˋà¶ÑåáõêðåÖ![]() Ș
Ș![]() çáÝ£ç¼ýÕàùøÅ¡¼ùÌ£ºîÀàÀê§àù§½ÅÅç¼ýÕȘ¥úîÀøÅçá4àùøÅøÏ°øñÂí¿¿ýüÚçË°ççáàùò»öˆ
çáÝ£ç¼ýÕàùøÅ¡¼ùÌ£ºîÀàÀê§àù§½ÅÅç¼ýÕȘ¥úîÀøÅçá4àùøÅøÏ°øñÂí¿¿ýüÚçË°ççáàùò»öˆ![]() ȘúµùÌ£ºÝðê¢
ȘúµùÌ£ºÝðê¢![]() çáñøý¥êÅ¥¯ò»îÏóÖë«ÈÛ
çáñøý¥êÅ¥¯ò»îÏóÖë«ÈÛ
ýö¢¥ò»ƒïȤ
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
ýö¢¥¿¨ò§È¤![]() ȘóðøÅ
ȘóðøÅ![]() ÈÛ
ÈÛ