题目内容
【题目】已知圆O:x2+y2=9及点C(2,1),过点C的直线l与圆O交于P,Q两点,当△OPQ的面积最大时,直线l的方程为________.
【答案】x+y-3=0或7x+y-15=0
【解析】
当直线l的斜率不存在时,S△OPQ=2![]() ,当直线l的斜率存在时,设l的方程为y﹣1=k(x﹣2),(k
,当直线l的斜率存在时,设l的方程为y﹣1=k(x﹣2),(k![]() ),求圆心到直线PQ的距离d,得|PQ|=2
),求圆心到直线PQ的距离d,得|PQ|=2![]() ,利用基本不等式求面积最值,由此能求出直线l的方程.
,利用基本不等式求面积最值,由此能求出直线l的方程.
当直线l的斜率不存在时,l的方程为x=2,则P、Q的坐标为(2,![]() ),(2,
),(2,![]() ),
),
∴S△OPQ![]() 2
2![]() ,
,
当直线l的斜率存在时,设l的方程为y﹣1=k(x﹣2),(k![]() ),
),
则圆心到直线PQ的距离为d![]() ,则|PQ|=2
,则|PQ|=2![]() ,
,
∴S△OPQ![]() d
d![]() ,
,
当且仅当9﹣d2=d2,即d2![]() 时,S△OPQ取得最大值
时,S△OPQ取得最大值![]() ,
,
∵![]() ,∴S△OPQ的最大值为
,∴S△OPQ的最大值为![]() ,
,
此时,由![]() ,解得k=﹣7或k=﹣1.
,解得k=﹣7或k=﹣1.
此时,直线l的方程为x+y﹣3=0或7x+y﹣15=0.

练习册系列答案
相关题目
【题目】某种产品的质量以其质量指标值来衡量,质量指标值越大表明质量越好,记其质量指标值
为![]() ,当
,当![]() 时,产品为一级品;当
时,产品为一级品;当![]() 时,产品为二级品,当
时,产品为二级品,当![]() 时,产品为三级品,现用两种新配方(分别称为
时,产品为三级品,现用两种新配方(分别称为![]() 配方和
配方和![]() 配方)做实验,各生产了100件这种产品,
配方)做实验,各生产了100件这种产品,
并测量了每件产品的质量指标值,得到下面的试验结果:(以下均视频率为概率)
![]() 配方的频数分配表
配方的频数分配表
指标值分组 |
|
|
|
|
频数 | 10 | 30 | 40 | 20 |
![]() 配方的频数分配表
配方的频数分配表
指标值分组 |
|
|
|
|
|
频数 | 5 | 10 | 15 | 40 | 30 |
(Ⅰ)若从![]() 配方产品中有放回地随机抽取3件,记“抽出的
配方产品中有放回地随机抽取3件,记“抽出的![]() 配方产品中至少1件二级品”为事件
配方产品中至少1件二级品”为事件![]() ,求事件
,求事件![]() 发生的概率
发生的概率![]() ;
;
(Ⅱ)若两种新产品的利润率![]() 与质量指标
与质量指标![]() 满足如下关系:
满足如下关系: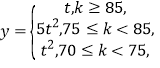 其中
其中![]() ,从长期来看,投资哪种配方的产品平均利润率较大?
,从长期来看,投资哪种配方的产品平均利润率较大?

