��Ŀ����
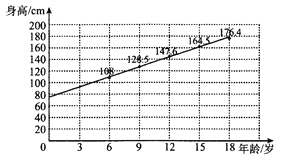
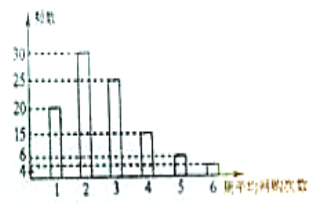
����Ŀ�������ǵ�ǰ���ڹ�����·�ʽ��ij��˾Ϊ�Ľ�Ӫ����ʽ�����������100������ͳ������ƽ�������Ĵ������������õ����µ�Ƶ���ֲ�ֱ��ͼ.��100�������У����䲻����40�����65�˽�������������ƽ������������С��4�ε������Ϊ�����ԣ�����֪������5����������䳬��40��.
��1��������֪������������![]() ���������ܷ��ڷ�����ĸ��ʲ�����0.10��ǰ������Ϊ�����������䲻����40���йأ�
���������ܷ��ڷ�����ĸ��ʲ�����0.10��ǰ������Ϊ�����������䲻����40���йأ�
������ | �������� | �ϼ� | |
���䲻����40�� | |||
���䳬��40�� | |||
�ϼ� |
��2������������������ѡȡ2�������������䳬��40�����������![]() �ķֲ���������.
�ķֲ���������.
���� 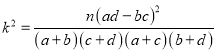 ��
��
| 0.15 | 0��10 | 0.05 | 0.01 |
| 2.072 | 2.706 | 3.841 | 6.635 |
���𰸡���1�������������2���������.
�����������������
(1)��������������������ɣ����![]()
![]() .���Կ����ڷ�����ĸ��ʲ�����0.10��ǰ������Ϊ�����������䲻����40���йأ�
.���Կ����ڷ�����ĸ��ʲ�����0.10��ǰ������Ϊ�����������䲻����40���йأ�
(2)�÷ֲ���Ϊ�����ηֲ���д���ֲ��пɵ�![]() .
.
���������
��1��������ɵ����������£�
������ | �������� | �ϼ� | |
���䲻����40�� | 20 | 45 | 65 |
���䳬��40�� | 5 | 30 | 35 |
�ϼ� | 25 | 75 | 100 |
���������������䲻����40��û�й�ϵ��
��![]()
![]() .
.
���Կ����ڷ�����ĸ��ʲ�����0.10��ǰ������Ϊ�����������䲻����40���йأ�
��2����Ƶ�ʷֲ�ֱ��ͼ��֪�������Թ���25��������������䳬��40����������![]() ������ȡֵΪ0��1��2��
������ȡֵΪ0��1��2��
![]() ��
�� ![]() ��
�� ![]() ��
��
![]()
![]() �ķֲ���Ϊ
�ķֲ���Ϊ
| 0 | 1 | 2 |
|
|
|
|
![]()
![]() .
.