Question

【题目】已知椭圆C1：y2＝1的左右顶点是双曲线C2：的顶点，且椭圆C1的上顶点到双曲线C2的渐近线的距离为．

（1）求双曲线C2的方程；

（2）若直线与C1相交于M1，M2两点，与C2相交于Q1，Q2两点，且5，求|M1M2|的取值范围．

Answer 1

【答案】（1）y2＝1；（2）|M1M2|∈（0，]．

【解析】

（1）由椭圆的顶点可得，求出双曲线的渐近线方程，运用点到直线的距离公式可得，进而得到双曲线的方程；

（2）设出直线的方程，联立双曲线方程，消去，运用韦达定理和判别式大于0，结合向量的数量积的坐标运算，求得的关系式，再由直线方程和椭圆的方程联立，运用韦达定理和弦长公式，即可求得的取值范围.

（1）由椭圆C1：y2＝1的左右顶点为（，0），（，0），可得a2＝3，

又椭圆C1的上顶点（0，1）到双曲线C2的渐近线bx﹣ay＝0的距离为，

由点到直线的距离公式有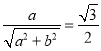可得b＝1，

所以双曲线C2的方程为y2＝1；

（2）易知直线l的斜率存在，设直线l的方程为y＝kx+m，

代入y2＝1，消去y并整理得（1﹣3k2）x2﹣6kmx﹣3m2﹣3＝0，

要与C2相交于两点，则应有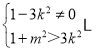①，

设Q1（x1，y1）、Q2（x2，y2），则有：x1+x2，x1x2．

又x1x2+y1y2＝x1x2+（kx1+m）（kx2+m）＝（1+k2）x1x2+km（x1+x2）+m2，

又5，所以有[（1+k2）（﹣3m2﹣3）+6k2m2+m2（1﹣3k2）]＝﹣5

整理得m2＝1﹣9k2…②，

将y＝kx+m，代入y2＝1，消去y并整理得：（1+3k2）x2+6kmx+3m2﹣3＝0，

要有两交点，则△＝36k2m2﹣4（1+3k2）（3m2﹣3）＞03k2+1＞m2…③

由①②③有：0＜k2．

设M1（x3，y3）、M2（x4，y4），则有：x3+x4，x3x4．

所以|M1M2|，

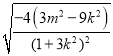又m2＝1﹣9k2，代入有：|M1M2|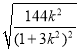|M1M2|

|M1M2|＝12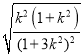，令t＝k2，则t∈（0，]，

令f（t）f′（t），又t∈（0，]，

所以f'（t）＞0在t∈（0，]内恒成立，故函数f（t）在t∈（0，]内单调递增，

故f（t）∈（0，]，则有|M1M2|∈（0，]．