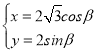题目内容
【题目】已知椭圆E:![]() (
(![]() )的焦距为
)的焦距为![]() ,直线
,直线![]() :
:![]() 与x轴的交点为G,过点
与x轴的交点为G,过点![]() 且不与x轴重合的直线
且不与x轴重合的直线![]() 交E于点A,B.当
交E于点A,B.当![]() 垂直x轴时,
垂直x轴时,![]() 的面积为
的面积为![]() .
.
(1)求E的方程;
(2)若![]() ,垂足为C,直线
,垂足为C,直线![]() 交x轴于点D,证明:
交x轴于点D,证明:![]() .
.
【答案】(1)![]() ;(2)证明见解析;
;(2)证明见解析;
【解析】
(1)由题意可得![]() ,即
,即![]() ,由三角形的面积公式可得
,由三角形的面积公式可得![]() ,由
,由![]() 在椭圆上,代入椭圆方程,解方程可得
在椭圆上,代入椭圆方程,解方程可得![]() ,
,![]() ,进而得到椭圆方程;
,进而得到椭圆方程;
(2)设直线![]() 的方程为
的方程为![]() ,联立椭圆方程,设
,联立椭圆方程,设![]() ,
,![]() ,
,![]() ,运用韦达定理,求得直线
,运用韦达定理,求得直线![]() 的方程,可令
的方程,可令![]() ,求得
,求得![]() ,再与
,再与![]() 作差,计算可得证明.
作差,计算可得证明.
解:(1)由焦距为![]() ,可得
,可得![]() ,即
,即![]() ,即
,即![]() ,①
,①
由题意可得![]() ,
,![]() ,
,
可得![]() ,由
,由![]() 在椭圆上,可得
在椭圆上,可得![]() ,②
,②
由①②解得![]() ,
,![]() ,
,
则椭圆的方程为![]() ;
;
(2)证明:过点![]() 且不与
且不与![]() 轴重合的直线
轴重合的直线![]() 的方程为
的方程为![]() ,
,
联立椭圆方程![]() ,可得
,可得![]() ,
,
设![]() ,
,![]() ,
,![]() ,
,
则![]() ,
,![]() ,
,
可得直线![]() 的方程为
的方程为![]() ,
,
令![]() ,可得
,可得![]() ,
,
由![]() ,
,
![]() ,可得
,可得![]() ,
,
则![]() .
.

 名校通行证有效作业系列答案
名校通行证有效作业系列答案【题目】某校倡导为特困学生募捐,要求在自动购水机处每购买一瓶矿泉水,便自觉向捐款箱中至少投入一元钱.现统计了连续5天的售出矿泉水箱数和收入情况,列表如下:
售出水量 | 7 | 6 | 6 | 5 | 6 |
收入 | 165 | 142 | 148 | 125 | 150 |
学校计划将捐款以奖学金的形式奖励给品学兼优的特困生,规定:特困生综合考核前20名,获一等奖学金500元;综合考核21-50名,获二等奖学金300元;综合考核50名以后的不获得奖学金.
(1)若![]() 与
与![]() 成线性相关,则某天售出9箱水时,预计收入为多少元?
成线性相关,则某天售出9箱水时,预计收入为多少元?
(2)假设甲、乙、丙三名学生均获奖,且各自获一等奖和二等奖的可能性相同,求三人获得奖学金之和不超过1000元的概率.
附:回归方程![]() ,其中
,其中 .
.
【题目】某单位为促进职工业务技能提升,对该单位120名职工进行一次业务技能测试,测试项目共5项.现从中随机抽取了10名职工的测试结果,将它们编号后得到它们的统计结果如下表(表1)所示(“√”表示测试合格,“×”表示测试不合格).
表1:
编号\测试项目 | 1 | 2 | 3 | 4 | 5 |
1 | × | √ | √ | √ | √ |
2 | √ | √ | √ | √ | × |
3 | √ | √ | √ | √ | × |
4 | √ | √ | √ | × | × |
5 | √ | √ | √ | √ | √ |
6 | √ | × | × | √ | × |
7 | × | √ | √ | √ | × |
8 | √ | × | × | × | × |
9 | √ | √ | × | × | × |
10 | √ | √ | √ | √ | × |
规定:每项测试合格得5分,不合格得0分.
(1)以抽取的这10名职工合格项的项数的频率代替每名职工合格项的项数的概率.
①设抽取的这10名职工中,每名职工测试合格的项数为![]() ,根据上面的测试结果统计表,列出
,根据上面的测试结果统计表,列出![]() 的分布列,并估计这120名职工的平均得分;
的分布列,并估计这120名职工的平均得分;
②假设各名职工的各项测试结果相互独立,某科室有5名职工,求这5名职工中至少有4人得分不少于20分的概率;
(2)已知在测试中,测试难度的计算公式为![]() ,其中
,其中![]() 为第
为第![]() 项测试难度,
项测试难度,![]() 为第
为第![]() 项合格的人数,
项合格的人数,![]() 为参加测试的总人数.已知抽取的这10名职工每项测试合格人数及相应的实测难度如下表(表2):
为参加测试的总人数.已知抽取的这10名职工每项测试合格人数及相应的实测难度如下表(表2):
表2:
测试项目 | 1 | 2 | 3 | 4 | 5 |
实测合格人数 | 8 | 8 | 7 | 7 | 2 |
定义统计量![]() ,其中
,其中![]() 为第
为第![]() 项的实测难度,
项的实测难度,![]() 为第
为第![]() 项的预测难度(
项的预测难度(![]() ).规定:若
).规定:若![]() ,则称该次测试的难度预测合理,否则为不合理,测试前,预估了每个预测项目的难度,如下表(表3)所示:
,则称该次测试的难度预测合理,否则为不合理,测试前,预估了每个预测项目的难度,如下表(表3)所示:
表3:
测试项目 | 1 | 2 | 3 | 4 | 5 |
预测前预估难度 | 0.9 | 0.8 | 0.7 | 0.6 | 0.4 |
判断本次测试的难度预估是否合理.