题目内容
5.如果函数f(x)=(a2-2)x在R上是减函数,那么实数a的取值范围是( )| A. | |a|>$\sqrt{2}$ | B. | $\sqrt{2}$<|a|<$\sqrt{3}$ | C. | |a|>$\sqrt{3}$ | D. | |a|<3 |
分析 根据指数函数的单调性便可得到0<a2-2<1,解该不等式便可得出|a|的范围,从而找出正确选项.
解答 解:f(x)在R是减函数;
∴0<a2-2<1;
∴2<a2<3;
∴$\sqrt{2}<|a|<\sqrt{3}$.
故选B.
点评 考查指数函数的单调性,以及不等式的性质.

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
20.总体由编号为01,02,…,29,30的30个个体组成.利用下面的随机数表选取4个个体,选取方法是如下从随机数表第2行的第2列数字0开始由左到右依次选取两个数字,则选出来的第3个个体的编号为20.
| 78 16 65 72 08 02 63 14 07 02 43 69 69 38 74 |
| 32 04 94 23 49 55 80 20 36 35 48 69 97 28 01 |
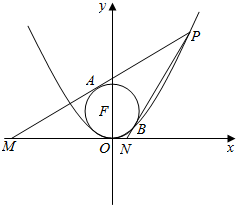 (文科)如图,已知抛物线C:y=$\frac{1}{4}$x2,点P(x0,y0)为抛物线上一点,y0∈[3,5],圆F方程为x2+(y-1)2=1,过点P作圆F的两条切线PA,PB分别交x轴于点M,N,切点分别为A,B.
(文科)如图,已知抛物线C:y=$\frac{1}{4}$x2,点P(x0,y0)为抛物线上一点,y0∈[3,5],圆F方程为x2+(y-1)2=1,过点P作圆F的两条切线PA,PB分别交x轴于点M,N,切点分别为A,B.