题目内容
15.设函数f(x)(x∈R)满足f(-x)=f(x),f(x)=f(2-x),且当x∈[0,1]时,f(x)=x2.又函数g(x)=|sin(πx)|,则函数h(x)=g(x)-f(x)在区间[-1,3]上零点的个数为( )| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
分析 根据条件判断函数f(x)的周期性,令h(x)=0,得g(x)=f(x),分别作出函数f(x)和g(x)的图象,利用图象判断两个函数的交点个数即可得到结论.
解答 解:∵f(-x)=f(x),f(x)=f(2-x),
∴f(x)=f(2-x)=f(x-2),
即函数是偶函数,且函数是周期为2的周期数列,
设x∈[-1,0],则-x∈[0,1],
则f(x)=f(-x)=(-x)2=x2,
即f(x)=x2.x∈[-1,1],
由h(x)=g(x)-f(x)=0,则f(x)=g(x),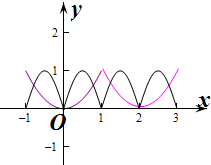
∵g(x)=|sin(πx)|,
∴在坐标系中作出函数f(x),g(x)的图象如图:
由图象可知,两个图象的交点个数为6个,
故函数h(x)=g(x)-f(x)在区间[-1,3]上零点的个数为6个,
故选:A
点评 本题主要考查函数零点个数的判断,利用数形结合转化为两个函数的图象交点个数是解决本题的关键.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案
相关题目
4.双曲线C:$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$的渐近线方程为$y=±\frac{{\sqrt{3}}}{2}x$,则C的离心率为( )
| A. | $\sqrt{5}$ | B. | $\frac{{\sqrt{7}}}{2}$ | C. | $\sqrt{7}$ | D. | $\frac{{\sqrt{21}}}{3}$ |
 中,平面
中,平面 平面
平面 ,
, ,
, .
. 平面
平面 ;
; 与平面
与平面 所成二面角的余弦值.
所成二面角的余弦值.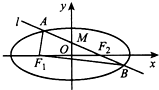 如图,椭圆C的左、右焦点分别为F1、F2,过F2的直线l交C于A,B两点,△ABF1的周长为8,且F2与抛物线y2=4x的焦点重合.
如图,椭圆C的左、右焦点分别为F1、F2,过F2的直线l交C于A,B两点,△ABF1的周长为8,且F2与抛物线y2=4x的焦点重合.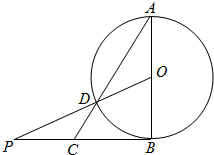 如图,AB为圆O的直径,O为圆心,PB与圆O相切于点B,PO交圆O于点D,AD的延长线交PB于点C,若AB=2,$PB=2\sqrt{2}$,则BC=$\sqrt{2}$.
如图,AB为圆O的直径,O为圆心,PB与圆O相切于点B,PO交圆O于点D,AD的延长线交PB于点C,若AB=2,$PB=2\sqrt{2}$,则BC=$\sqrt{2}$. 如图,圆锥的顶点为P,底面圆为O,底面的一条直径为AB,C为半圆弧$\widehat{AB}$的中点,E为劣弧$\widehat{CB}$的中点,已知PO=2,OA=1,求三棱锥P-AOC的体积,并求异面直线PA和OE所成角的大小.
如图,圆锥的顶点为P,底面圆为O,底面的一条直径为AB,C为半圆弧$\widehat{AB}$的中点,E为劣弧$\widehat{CB}$的中点,已知PO=2,OA=1,求三棱锥P-AOC的体积,并求异面直线PA和OE所成角的大小.