题目内容
19.由不等式组$\left\{\begin{array}{l}{2x-y-2≥0}\\{x-2y+4≥0}\\{x-1≤0}\end{array}\right.$确定的平面区域记为M,若直线3x-2y+a=0与M有公共点,则a的最大值为( )| A. | -3 | B. | 1 | C. | 2 | D. | 4 |
分析 作出不等式对应的平面区域,利用线性规划的知识,通过平移即可求a的最大值.
解答 解:作出不等式组对应的平面区域如图:(阴影部分).
由3x-2y+a=0得y=$\frac{3}{2}$x+$\frac{a}{2}$,
平移直线y=$\frac{3}{2}$x+$\frac{a}{2}$,
由图象可知当直线y=$\frac{3}{2}$x+$\frac{a}{2}$经过点A时,直线y=$\frac{3}{2}$x+$\frac{a}{2}$的截距最大,
此时a最大.
由$\left\{\begin{array}{l}{x=1}\\{2x-y-2=0}\end{array}\right.$得$\left\{\begin{array}{l}{x=1}\\{y=0}\end{array}\right.$,即A(1,0),
代入3x-2y+a=0得3+a=0.
解得a=-3,
即a的最大值为-3.
故选:A
点评 本题主要考查线性规划的应用,利用图象平行,利用数形结合是解决线性规划问题中的基本方法.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案
相关题目
14. 棱长为2的正方体被一平面截成两个几何体,其中一个几何体的三视图如图所示,那么该几何体的体积是( )
棱长为2的正方体被一平面截成两个几何体,其中一个几何体的三视图如图所示,那么该几何体的体积是( )
 棱长为2的正方体被一平面截成两个几何体,其中一个几何体的三视图如图所示,那么该几何体的体积是( )
棱长为2的正方体被一平面截成两个几何体,其中一个几何体的三视图如图所示,那么该几何体的体积是( )| A. | $\frac{10}{3}$ | B. | 3 | C. | $\frac{14}{3}$ | D. | 4 |
4.双曲线C:$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$的渐近线方程为$y=±\frac{{\sqrt{3}}}{2}x$,则C的离心率为( )
| A. | $\sqrt{5}$ | B. | $\frac{{\sqrt{7}}}{2}$ | C. | $\sqrt{7}$ | D. | $\frac{{\sqrt{21}}}{3}$ |
 有且只有两个零点,则实数
有且只有两个零点,则实数 的取值集合为( )
的取值集合为( ) B.
B.
 D.
D.
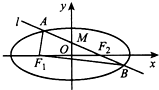 如图,椭圆C的左、右焦点分别为F1、F2,过F2的直线l交C于A,B两点,△ABF1的周长为8,且F2与抛物线y2=4x的焦点重合.
如图,椭圆C的左、右焦点分别为F1、F2,过F2的直线l交C于A,B两点,△ABF1的周长为8,且F2与抛物线y2=4x的焦点重合.