题目内容
已知x,y满足条件
(1)求z=2y-x的最大值.
(2)求x2+y2的最小值.
|
(1)求z=2y-x的最大值.
(2)求x2+y2的最小值.
(1)作出不等式组
表示的平面区域,
得到如图的△ABC及其内部,其中A(1,3),B(7,9),C(3,1),
设z=F(x,y)=2y-x,将直线l:z=2y-x进行平移,
观察x轴上的截距变化,可得当l经过点BC上一点时,目标函数z达到最大值.
∴z最大值=F(7,9)=11;
(2)设P(x,y)为区域内一个动点,
则|OP|=
,因此x2+y2=|OP|2表示O、P两点距离的平方之值.
∵当P与原点O在AC上的射影Q重合时,|OP|=
=2
达到最小值
∴|OP|2的最小值为8,即x2+y2的最小值为8.
|

得到如图的△ABC及其内部,其中A(1,3),B(7,9),C(3,1),
设z=F(x,y)=2y-x,将直线l:z=2y-x进行平移,
观察x轴上的截距变化,可得当l经过点BC上一点时,目标函数z达到最大值.
∴z最大值=F(7,9)=11;
(2)设P(x,y)为区域内一个动点,
则|OP|=
| x2+y2 |
∵当P与原点O在AC上的射影Q重合时,|OP|=
| |0+0-4| | ||
|
| 2 |
∴|OP|2的最小值为8,即x2+y2的最小值为8.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
 满足
满足 ,则点
,则点 表示区域的面积为( )
表示区域的面积为( )



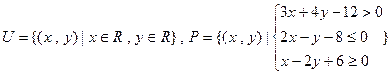 ,
,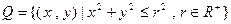 ,若
,若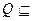 CUP恒成立,则实数
CUP恒成立,则实数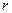 最大值是( )
最大值是( )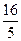 C.
C. 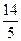 C.
C. 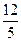
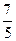
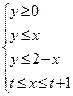 所确定的区域面积为S,记
所确定的区域面积为S,记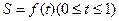 ,则
,则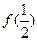 =▲
=▲

