题目内容
表面积为4
的正四面体的各个顶点都在同一个球面上,则此球的体积为( )
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:球的体积和表面积,球内接多面体
专题:空间位置关系与距离
分析:将正四面体补成正方体,再将正方体放在一个球体中,利用它们之间的关系求解.
解答:
 解:如图,将正四面体补形成一个正方体,
解:如图,将正四面体补形成一个正方体,
∵表面积为4
的正四面体,
正四面体棱长为A,
a2=
,解得a=2,
∴正方体的棱长是
,
又∵球的直径是正方体的对角线,设球半径是R,
∴2R=
,
∴R=
,
∴球的体积为
π(
)3=
π.
故选:C.
 解:如图,将正四面体补形成一个正方体,
解:如图,将正四面体补形成一个正方体,∵表面积为4
| 3 |
正四面体棱长为A,
| ||
| 4 |
| 3 |
∴正方体的棱长是
| 2 |
又∵球的直径是正方体的对角线,设球半径是R,
∴2R=
| 6 |
∴R=
| ||
| 2 |
∴球的体积为
| 4 |
| 3 |
| ||
| 2 |
| 6 |
故选:C.
点评:巧妙构造正方体,利用正方体的外接球的直径为正方体的对角线,从而将问题巧妙转化.若已知正四面体V-ABC的棱长为a,求外接球的半径,可以构造出一个球的内接正方体,再应用对角线长等于球的直径可求得.

练习册系列答案
相关题目
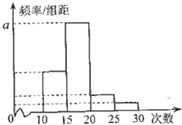 对某校高二年级学生参加社区服务次数进行统计,随机抽取M名学生作为样本,得到这M名学生参加社区服务的次数根据此数据作出了频数与频率的统计表和频率分布直方图如下:
对某校高二年级学生参加社区服务次数进行统计,随机抽取M名学生作为样本,得到这M名学生参加社区服务的次数根据此数据作出了频数与频率的统计表和频率分布直方图如下: