题目内容
二维空间中圆的一维测度(周长)l＝2πr，二维测度(面积)S＝πr2，观察发现S′＝l；三维空间中球的二维测度(表面积)S＝4πr2，三维测度(体积)V＝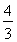
πr3，观察发现V′＝S.则由四维空间中“超球”的三维测度V＝8πr3，猜想其四维测度W＝________.
2πr4.
【解析】依题意猜想其四维测度的导数W′＝V＝8πr3，故可得W＝2πr4.
练习册系列答案
相关题目
题目内容
二维空间中圆的一维测度(周长)l＝2πr，二维测度(面积)S＝πr2，观察发现S′＝l；三维空间中球的二维测度(表面积)S＝4πr2，三维测度(体积)V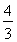＝πr3，观察发现V′＝S.则由四维空间中“超球”的三维测度V＝8πr3，猜想其四维测度W＝________.
2πr4.
【解析】依题意猜想其四维测度的导数W′＝V＝8πr3，故可得W＝2πr4.
