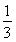题目内容
某创业投资公司拟投资开发某种新能源产品,估计能获得10万元到1 000万元的投资收益.现准备制定一个对科研课题组的奖励方案:资金y(单位:万元)随投资收益x(单位:万元)的增加而增加,且奖金不超过9万元,同时奖金不超过投资收益的20%.
(1)若建立函数y=f(x)模型制定奖励方案,试用数学语言表述该公司对奖励函数f(x)模型的基本要求,并分析函数y=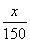 +2是否符合公司要求的奖励函数模型,并说明原因;
+2是否符合公司要求的奖励函数模型,并说明原因;
(2)若该公司采用模型函数y=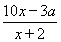 作为奖励函数模型,试确定最小的正整数a的值.
作为奖励函数模型,试确定最小的正整数a的值.
(1)不符合公司要求(2)328
【解析】(1)设奖励函数模型为y=f(x),按公司对函数模型的基本要求,函数y=f(x)满足:
当x∈[10,1 000]时,
①f(x)在定义域[10,1 000]上是增函数;
②f(x)≤9恒成立;
③f(x)≤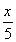 恒成立.(2分)
恒成立.(2分)
对于函数模型f(x)=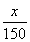 +2.
+2.
当x∈[10,1 000]时,f(x)是增函数,(3分)
f(x)max=f(1 000)=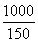 +2=
+2=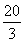 +2<9.
+2<9.
所以f(x)≤9恒成立.
但x=10时,f(10)=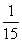 +2>
+2>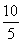 ,即f(x)≤
,即f(x)≤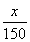 不恒成立,
不恒成立,
故该函数模型不符合公司要求.(6分)
(2)对于函数模型f(x)=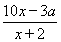 ,即f(x)=10-
,即f(x)=10-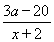 ,
,
当3a+20>0,即a>-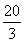 时递增;(8分)
时递增;(8分)
要使f(x)≤9对x∈[10,1 000]恒成立,
即f(1 000)≤9,3a+18≥1 000,a≥ ;(10分)
;(10分)
要使f(x)≤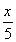 对x∈[10,1 000]恒成立,
对x∈[10,1 000]恒成立,
即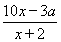 ≤
≤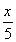 ,x2-48x+15a≥0恒成立,所以a≥
,x2-48x+15a≥0恒成立,所以a≥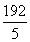 .(12分)
.(12分)
综上所述,a≥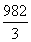 ,所以满足条件的最小的正整数a的值为328.(14分)
,所以满足条件的最小的正整数a的值为328.(14分)

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目