题目内容
11.已知f(x)=lg$\frac{2x}{ax+b}$,且f(1)=0,对任意的x>0时,恒有f(x)-f($\frac{1}{x}$)=lgx.(1)求f(x)的解析式;
(2)判断并用定义域证明f(x)的单调性.
分析 (1)当x>0时,恒有f(x)-f($\frac{1}{x}$)=lgx,可以构造一个关于a,b方程组,解方程组求出a,b值,进而求出函数的解析式;(2)根据单调性的定义证明即可.
解答 解:(1)∵当x>0时,有f(x)-f($\frac{1}{x}$)=lgx恒成立,
∴lg $\frac{2x}{ax+b}$-lg $\frac{\frac{2}{x}}{\frac{a}{x}+b}$=lgx,
即lg $\frac{2x}{ax+b}$-lg $\frac{2}{a+bx}$=lgx,
即lg( $\frac{2x}{ax+b}$•$\frac{a+bx}{2}$)=lgx,$\frac{(a+bx)x}{ax+b}$=x.
整理得(a-b)x2-(a-b)x=0恒成立,
∴a=b,
又f(1)=0,
即a+b=2,从而a=b=1,
∴f(x)=lg$\frac{2x}{x+1}$;
(2)由(1)得:$\frac{2x}{x+1}$>0,解得:x>0或x<-1,
∴函数的定义域是(-∞,-1)∪(0,+∞),
设x1>x2>0,
则f(x1)-f(x2)
=lg$\frac{{2x}_{1}}{{x}_{1}+1}$-lg$\frac{{2x}_{2}}{{x}_{2}+1}$
=lg$\frac{1+\frac{1}{{x}_{2}}}{1+\frac{1}{{x}_{1}}}$,
∵x1>x2>0,
∴$\frac{1}{{x}_{1}}$+1<$\frac{1}{{x}_{2}}$+1,
∴lg$\frac{1+\frac{1}{{x}_{2}}}{1+\frac{1}{{x}_{1}}}$>0,
∴f(x1)-f(x2)>0,
∴f(x)在(0,+∞)递增,
同理可证f(x)在(-∞,-1)递增.
点评 本题主要考查对数的基本运算,求函数的解析式问题,函数单调性定义的应用,根据条件建立方程组是解决本题的关键.

| A. | {x≠0或≠2} | B. | (-∞,0)∪(2,+∞) | C. | (-∞,0]∪[2,+∞) | D. | (0,2) |
| A. | {锐角三角形} | B. | {钝角三角形} | C. | {直角三角形} | D. | {三角形} |
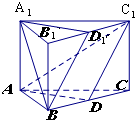 如图所示,已知三棱柱ABC-A1B1C1中,D是BC的中点,D1是B1C1的中点,设平面A1D1B∩平面ABC=l1,平面ADC1∩平面A1B1C1=l2,求证:l1∥l2.
如图所示,已知三棱柱ABC-A1B1C1中,D是BC的中点,D1是B1C1的中点,设平面A1D1B∩平面ABC=l1,平面ADC1∩平面A1B1C1=l2,求证:l1∥l2.