题目内容
1．
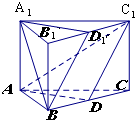如图所示，已知三棱柱ABC-A1B1C1中，D是BC的中点，D1是B1C1的中点，设平面A1D1B∩平面ABC=l1，平面ADC1∩平面A1B1C1=l2，求证：l1∥l2．
分析 连接DD1．过B点作直线l1'∥AD，证明l1'即为l1，可得l1∥AD∥A1D1；过C1作直线l2'∥A1D1，证明l2'即为l2，l2∥AD∥A1D1；即可得证l1∥l2．
解答 证明：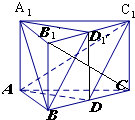
连接DD1．在四边形BDD1B1中，BD=$\frac{1}{2}$BC=$\frac{1}{2}$B1C1=B1D1，BD∥B1D1，
所以四边形BDD1B1为平行四边形，
所以DD1=BB1=AA1①，且DD1∥BB1∥AA1②；由①、②得：四边形ADD1A1为平行四边形，
所以AD∥A1D1③；
过B点作直线l1'∥AD，由③知l1'∥A1D1，由于AD在面ABC中，A1D1在面A1B1C1中，
所以l1'∥面ABC，l1'∥A1B1C1，由于B点同时在面ABC和面A1B1C1中，
所以l1'同时在面ABC和面A1B1C1中，即l1'为面ABC和面A1B1C1的交线，
所以l1'即为l1，
所以l1∥AD∥A1D1④；
过C1作直线l2'∥A1D1，同上可以证明l2'即为l2，l2∥AD∥A1D1⑤；
由④、⑤即得l1∥l2．
点评 本题在三棱柱中证明面面平行，并且证明了线面垂直．着重考查了线面平行、面面平行的判定定理，线面垂直的判定与性质等知识，属于中档题．
练习册系列答案
相关题目