题目内容
1.作出下列函数的图象,并写出函数的单调区间.(1)y=(x+2)|x-1|;
(2)y=$\frac{{(x+\frac{1}{2})}^{0}}{|x|-x}$.
分析 (1)化简y=(x+2)|x-1|=$\left\{\begin{array}{l}{-(x+2)(x-1),x≤1}\\{(x+2)(x-1),x>1}\end{array}\right.$,从而作函数的图象,再写出函数的单调区间.
(2)化简y=$\frac{{(x+\frac{1}{2})}^{0}}{|x|-x}$=$\frac{1}{|x|-x}$=$\frac{1}{-2x}$,(x<0且x≠$-\frac{1}{2}$),从而作函数的图象,再写出函数的单调区间.
解答 解:(1)y=(x+2)|x-1|=$\left\{\begin{array}{l}{-(x+2)(x-1),x≤1}\\{(x+2)(x-1),x>1}\end{array}\right.$;
作函数的图象如下,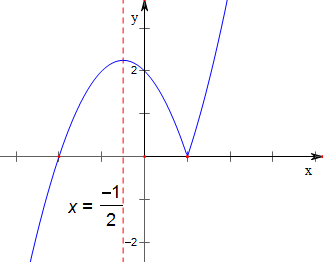
其单调减区间为[-$\frac{1}{2}$,1],单调增区间为(-∞,-$\frac{1}{2}$),(1,+∞);
(2)y=$\frac{{(x+\frac{1}{2})}^{0}}{|x|-x}$=$\frac{1}{|x|-x}$=$\frac{1}{-2x}$,(x<0且x≠$-\frac{1}{2}$).
作函数的图象如下,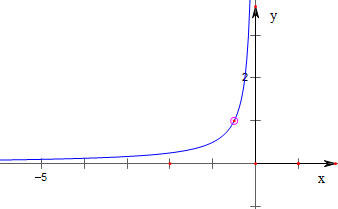
其单调增区间为(-∞,-$\frac{1}{2}$),(-$\frac{1}{2}$,0).
点评 本题考查了绝对值函数的及分段函数的应用,同时考查了数形结合的思想应用.

练习册系列答案
相关题目