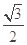题目内容
在锐角 中,
中, 且
且 .
.
(1)求 的大小;
的大小;
(2)若 ,求
,求 的值.
的值.
 中,
中, 且
且 .
.(1)求
 的大小;
的大小;(2)若
 ,求
,求 的值.
的值.(1) ;(2)若
;(2)若 ,则
,则 的值不存在.
的值不存在.
 ;(2)若
;(2)若 ,则
,则 的值不存在.
的值不存在.试题分析:(1)求
 的大小,求角的大小,可用正弦定理来求,也可利用余弦定理来求,本题由已知
的大小,求角的大小,可用正弦定理来求,也可利用余弦定理来求,本题由已知 且
且 ,即
,即 ,符合利用正弦定理来求,故由正弦定理得
,符合利用正弦定理来求,故由正弦定理得 ,利用三角形
,利用三角形 为锐角三角形,即可求出角
为锐角三角形,即可求出角 的值;(2)若
的值;(2)若 ,求
,求 的值,由于已知
的值,由于已知 ,可利用余弦定理来求边长
,可利用余弦定理来求边长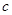 ,注意,求出后要验证三角形是否为锐角.
,注意,求出后要验证三角形是否为锐角.(1)由正弦定理可得
 2分
2分因为

所以
 5分
5分在锐角
 中,
中, 7分
7分(2)由余弦定理可得
 9分
9分又因为

所以
 ,即
,即 11分
11分解得
 12分
12分经检验,由
 可得
可得 ,不符合题意,
,不符合题意,所以
 舍去. 13分
舍去. 13分
练习册系列答案
相关题目
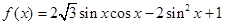 .
.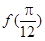 的值;
的值;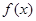 在区间
在区间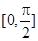 上的最大值和最小值.
上的最大值和最小值. ,
,  ,则
,则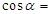 。
。 的取值范围是_______ .
的取值范围是_______ . .
. ,且
,且 ,求角
,求角 的值;
的值; ,且
,且 ,求
,求 的值.
的值. 是
是 边
边 延长线上一点,记
延长线上一点,记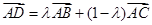 . 若关于
. 若关于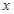 的方程
的方程 在
在 上恰有两解,则实数
上恰有两解,则实数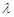 的取值范围是( )
的取值范围是( )
 或
或
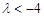 或
或 的值为( )
的值为( )