题目内容
已知向量
=(a,b),
=(sin2x,2cos2x),若f(x)=
•
,且f(0)=8,f(
)=12.
(1)求a,b的值;
(2)求函数f(x)的最大值及取得最大值时的x的集合;
(3)求函数f(x)的单调增区间.
| m |
| n |
| m |
| n |
| π |
| 6 |
(1)求a,b的值;
(2)求函数f(x)的最大值及取得最大值时的x的集合;
(3)求函数f(x)的单调增区间.
(1)由题意可知f(x)=asin2x+2bcos2x
由f(0)=2b=8,解得b=4.
由f(
)=asin
+2bcos2
=
a+8×
=12,解得a=4
.
(2)由(1)可知f(x)=4
sin2x+4cos2x+4=8(
sin2x+
cos2x)+4
∴f(x)=8sin(2x+
)+4.
当2x+
=2kπ+
,k∈Z时,sin(2x+
)取得最大值1,
∴f(x)max=8×1+4=12
此时x的集合为{x|x=kπ+
,k∈Z}.
(3)由-
+2kπ≤2x+
≤2kπ+
(k∈Z),
解得kπ-
≤x≤kπ+
(k∈Z).
∴函数f(x)的单调增区间是[kπ-
,kπ+
](k∈Z).
由f(0)=2b=8,解得b=4.
由f(
| π |
| 6 |
| π |
| 3 |
| π |
| 6 |
| ||
| 2 |
| 3 |
| 4 |
| 3 |
(2)由(1)可知f(x)=4
| 3 |
| ||
| 2 |
| 1 |
| 2 |
∴f(x)=8sin(2x+
| π |
| 6 |
当2x+
| π |
| 6 |
| π |
| 2 |
| π |
| 6 |
∴f(x)max=8×1+4=12
此时x的集合为{x|x=kπ+
| π |
| 6 |
(3)由-
| π |
| 2 |
| π |
| 6 |
| π |
| 2 |
解得kπ-
| π |
| 3 |
| π |
| 6 |
∴函数f(x)的单调增区间是[kπ-
| π |
| 3 |
| π |
| 6 |

练习册系列答案
相关题目
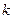 ,使方程
,使方程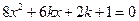 的两个根是一个直角三角形的两个锐角的正弦值.
的两个根是一个直角三角形的两个锐角的正弦值. 中,
中, 且
且 .
. 的大小;
的大小; ,求
,求 的值.
的值.