题目内容
 是
是 边
边 延长线上一点,记
延长线上一点,记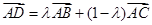 . 若关于
. 若关于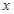 的方程
的方程 在
在 上恰有两解,则实数
上恰有两解,则实数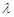 的取值范围是( )
的取值范围是( )A. | B. 或 或 |
C. | D.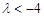 或 或 |
D
试题分析:
 在
在 边
边 延长线上,因此由
延长线上,因此由 ,知
,知 ,故
,故 ,由于
,由于 都不是原方程的解,故原方程在
都不是原方程的解,故原方程在 上恰有两解,这等价于
上恰有两解,这等价于 在
在 上恰有两解,令
上恰有两解,令 ,即要求
,即要求 在
在 上恰有两解,故当直线
上恰有两解,故当直线 与
与 (“双钩”或称“耐克”型函数)恰有一个交点时符合题意,因为当
(“双钩”或称“耐克”型函数)恰有一个交点时符合题意,因为当 时
时 在
在 始终恰好有两个解
始终恰好有两个解 .
.
 时
时 ;又
;又 ,故只需考虑
,故只需考虑 时的情况,
时的情况, 在
在 上递增,在
上递增,在 上递减,
上递减, ,
, ,故当
,故当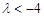 或
或 时直线
时直线 与
与 恰有一个交点,即原方程恰好2解.
恰有一个交点,即原方程恰好2解.
练习册系列答案
 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案
相关题目
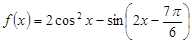 .
.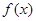 的最大值,并写出
的最大值,并写出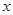 的取值集合;
的取值集合;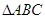 中,角
中,角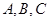 的对边分别为
的对边分别为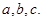 若
若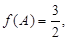
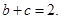 求实数
求实数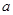 的最小值.
的最小值. 中,
中, 且
且 .
. 的大小;
的大小; ,求
,求 的值.
的值.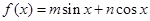 ,且
,且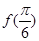 是它的最大值,(其中m、n为常数且
是它的最大值,(其中m、n为常数且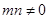 )给出下列命题:①
)给出下列命题:①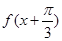 是偶函数;②函数
是偶函数;②函数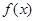 的图象关于点
的图象关于点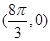 对称;③
对称;③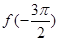 是函数
是函数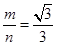 .
.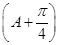 =
=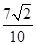 ,A∈
,A∈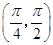 .
.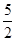 sinAsinx的值域.
sinAsinx的值域. )来表示(x为月份),已知3月份达到最高价9万元,7月份价格最低,为5万元,则国庆节期间的价格约为( )
)来表示(x为月份),已知3月份达到最高价9万元,7月份价格最低,为5万元,则国庆节期间的价格约为( ) sin x,sin x),b=(cos x,sin x),x∈
sin x,sin x),b=(cos x,sin x),x∈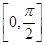 .
. 在直线
在直线 上,则
上,则 的值等于 。
的值等于 。