题目内容
【题目】已知点![]() 是抛物线
是抛物线![]() :
:![]() 上的一点,其焦点为点
上的一点,其焦点为点![]() ,且抛物线
,且抛物线![]() 在点
在点![]() 处的切线
处的切线![]() 交圆
交圆![]() :
:![]() 于不同的两点
于不同的两点![]() ,
,![]() .
.
(1)若点![]() ,求
,求![]() 的值;
的值;
(2)设点![]() 为弦
为弦![]() 的中点,焦点
的中点,焦点![]() 关于圆心
关于圆心![]() 的对称点为
的对称点为![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() (2)
(2)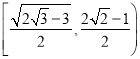
【解析】
(1)利用导数求出过点![]() 的抛物线的切线,切线与圆相交,根据弦心距、半径、弦长的关系求解即可;
的抛物线的切线,切线与圆相交,根据弦心距、半径、弦长的关系求解即可;
(2)设点![]() ,联立切线与圆的方程消元可得一元二次方程,由韦达定理求出中点
,联立切线与圆的方程消元可得一元二次方程,由韦达定理求出中点![]() 的坐标,由两点间距离公式表示出
的坐标,由两点间距离公式表示出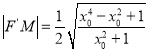 ,令
,令![]() 换元,利用函数的单调性即可求出取值范围.
换元,利用函数的单调性即可求出取值范围.
设点![]() ,其中
,其中![]() .
.
因为![]() ,所以切线
,所以切线![]() 的斜率为
的斜率为![]() ,于是切线
,于是切线![]() :
:![]() .
.
(1)因为![]() ,于是切线
,于是切线![]() :
:![]() .
.
故圆心![]() 到切线
到切线![]() 的距离为
的距离为![]() .
.
于是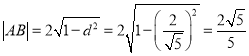 .
.
(2)联立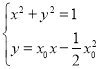 得
得![]() .
.
设![]() ,
,![]() ,
,![]() .则
.则![]() ,
,![]() .
.
解得![]()
又![]() ,于是
,于是![]() .
.
于是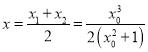 ,
,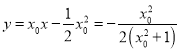 .
.
又![]() 的焦点
的焦点![]() ,于是
,于是![]() .
.
故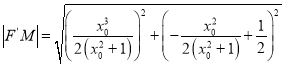
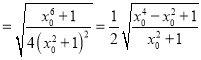 .
.
令![]() ,则
,则![]() .于是
.于是![]() .
.
因为![]() 在
在![]() 单调递减,在
单调递减,在![]() 单调递增.
单调递增.
又当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() .
.
所以![]() 的取值范围为
的取值范围为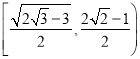 .
.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
【题目】某省即将实行新高考,不再实行文理分科.某校为了研究数学成绩优秀是否对选择物理有影响,对该校2018级的1000名学生进行调查,收集到相关数据如下:
(1)根据以上提供的信息,完成![]() 列联表,并完善等高条形图;
列联表,并完善等高条形图;
选物理 | 不选物理 | 总计 | |
数学成绩优秀 | |||
数学成绩不优秀 | 260 | ||
总计 | 600 | 1000 |
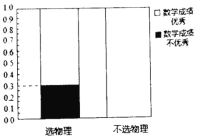
(2)能否在犯错误的概率不超过0.05的前提下认为数学成绩优秀与选物理有关?
附: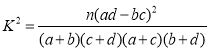
临界值表:
| 0.10 | 0.05 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |