题目内容
【题目】已知函数![]() .
.
(Ⅰ)求函数![]() 的单调区间与极值;
的单调区间与极值;
(Ⅱ)若不等式![]() 对任意
对任意![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(Ⅲ)求证:![]() .
.
【答案】(Ⅰ)见解析;(Ⅱ)![]() ;(Ⅲ)见解析.
;(Ⅲ)见解析.
【解析】
(Ⅰ)函数的定义域为![]() .且
.且 ![]() ,据此列表讨论可知:
,据此列表讨论可知:![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() .
.![]() 的极大值为
的极大值为![]() ,无极小值.
,无极小值.
(Ⅱ)由题意可得![]() 恒成立,令
恒成立,令![]() ,由导函数可得当
,由导函数可得当![]() 时函数
时函数![]() 有最大值
有最大值![]() ,所以
,所以![]() .
.
(Ⅲ)由(Ⅱ)知![]() ,则
,则![]() ,据此结合不等式的性质利用放缩法即可证得
,据此结合不等式的性质利用放缩法即可证得![]() .
.
(Ⅰ)定义域为![]() .
.
![]() ,令
,令![]() ,得
,得![]() .
.
|
|
|
|
|
| 0 |
|
| 增 | 极大值 | 减 |
由上图表知:
![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() .
.
![]() 的极大值为
的极大值为![]() ,无极小值.
,无极小值.
(Ⅱ)![]()
![]()
![]() ,令
,令![]() 又
又![]() ,
,
令![]() 解得
解得![]() ,当x在
,当x在![]() 内变化时,
内变化时,![]() ,
,![]() 变化如下表:
变化如下表:
x |
|
|
|
| + | 0 |
|
| ↗ |
| ↘ |
由表知,当![]() 时函数
时函数![]() 有最大值,且最大值为
有最大值,且最大值为![]() ,所以
,所以![]() .
.
(Ⅲ)由(Ⅱ)知![]() ,
,
![]()
![]()
![]()
![]() ,
,
又![]()
![]() ,
,
![]()
![]() ,
,
即![]() .
.

【题目】为了保障全国第四次经济普查顺利进行,国家统计局从东部选择江苏, 从中部选择河北. 湖北,从西部选择宁夏, 从直辖市中选择重庆作为国家综合试点地区,然后再逐级确定普查区域,直到基层的普查小区.在普查过程中首先要进行宣传培训,然后确定对象,最后入户登记. 由于种种情况可能会导致入户登记不够顺利,这为正式普查提供了宝贵的试点经验. 在某普查小区,共有 50 家企事业单位,150 家个体经营户,普查情况如下表所示:
普查对象类别 | 顺利 | 不顺利 | 合计 |
企事业单位 | 40 | 10 | 50 |
个体经营户 | 100 | 50 | 150 |
合计 | 140 | 60 | 200 |
(1)写出选择 5 个国家综合试点地区采用的抽样方法;
(2)根据列联表判断是否有![]() 的把握认为“此普查小区的入户登记是否顺利与普查对象的类别有关”;
的把握认为“此普查小区的入户登记是否顺利与普查对象的类别有关”;
(3)以频率作为概率, 某普查小组从该小区随机选择 1 家企事业单位,3 家个体经营户作为普查对象,入户登记顺利的对象数记为![]() , 写出
, 写出![]() 的分布列,并求
的分布列,并求![]() 的期望值.
的期望值.
附:![]()
| 0.10 | 0.010 | 0.001 |
| 2.706 | 6.635 | 10.88 |
【题目】某学生为了测试煤气灶烧水如何节省煤气的问题设计了一个实验,并获得了煤气开关旋钮旋转的弧度数![]() 与烧开一壶水所用时间
与烧开一壶水所用时间![]() 的一组数据,且作了一定的数据处理(如下表),得到了散点图(如下图).
的一组数据,且作了一定的数据处理(如下表),得到了散点图(如下图).
|
|
|
|
|
|
|
|
|
|
|
|
|
|
表中![]() ,
,![]() .
.

(1)根据散点图判断,![]() 与
与![]() 哪一个更适宜作烧水时间
哪一个更适宜作烧水时间![]() 关于开关旋钮旋转的弧度数
关于开关旋钮旋转的弧度数![]() 的回归方程类型?(不必说明理由)
的回归方程类型?(不必说明理由)
(2)根据判断结果和表中数据,建立![]() 关于
关于![]() 的回归方程;
的回归方程;
(3)若单位时间内煤气输出量![]() 与旋转的弧度数
与旋转的弧度数![]() 成正比,那么,利用第(2)问求得的回归方程知
成正比,那么,利用第(2)问求得的回归方程知![]() 为多少时,烧开一壶水最省煤气?
为多少时,烧开一壶水最省煤气?
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘法估计值分别为
的斜率和截距的最小二乘法估计值分别为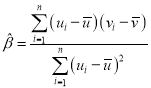 ,
,![]()
【题目】某品牌餐饮公司准备在10个规模相当的地区开设加盟店,为合理安排各地区加盟店的个数,先在其中5个地区试点,得到试点地区加盟店个数分别为1,2,3,4,5时,单店日平均营业额![]() (万元)的数据如下:
(万元)的数据如下:
加盟店个数 | 1 | 2 | 3 | 4 | 5 |
单店日平均营业额 | 10.9 | 10.2 | 9 | 7.8 | 7.1 |
(1)求单店日平均营业额![]() (万元)与所在地区加盟店个数
(万元)与所在地区加盟店个数![]() (个)的线性回归方程;
(个)的线性回归方程;
(2)根据试点调研结果,为保证规模和效益,在其他5个地区,该公司要求同一地区所有加盟店的日平均营业额预计值总和不低于35万元,求一个地区开设加盟店个数![]() 的所有可能取值;
的所有可能取值;
(3)小赵与小王都准备加入该公司的加盟店,根据公司规定,他们只能分别从其他五个地区(加盟店都不少于2个)中随机选一个地区加入,求他们选取的地区相同的概率.
(参考数据及公式:![]() ,
,![]() ,线性回归方程
,线性回归方程![]() ,其中
,其中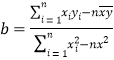 ,
,![]() .)
.)