题目内容
【题目】如图，直三棱柱ABC﹣A′B′C′中，AA′=2AC=2BC，E为AA′的中点，C′E⊥BE．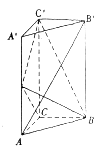 
（1）求证：C′E⊥平面BCE；
（2）若AC=2，求三棱锥B′﹣ECB的体积．
【答案】
（1）证明：在矩形A′ACC′中，E为A′A中点且AA′=2AC，
∴EA=AC，EA′=A′C′，
∴∠AEC=∠A′EC=45°，
∴C′E⊥EC，
∵C′E⊥BE，CE∩BE=E，
∴C′E⊥平面BCE；
（2）解：∵B′C′∥BC，B′C′平面BCE，BC平面BCE，
∴B′C′∥平面BCE，
∴VB′﹣ECB=VC′﹣ECB，
∵C′E⊥平面BCE，
∴C′E⊥BC，
∵BC⊥CC′，C′E∩CC′=C′，
∴BC⊥平面ACC′A′′∴BC⊥CE，
∵AC=2，
∴BC=2，EC=EC′=2 
，
∴VB′﹣ECB=VC′﹣ECB= 
= 
【解析】（1）证明C′E⊥EC，利用C′E⊥BE，CE∩BE=E，即可证明C′E⊥平面BCE；（2）利用等体积转化求三棱锥B′﹣ECB的体积．
【考点精析】解答此题的关键在于理解直线与平面平行的判定的相关知识，掌握平面外一条直线与此平面内的一条直线平行，则该直线与此平面平行；简记为：线线平行，则线面平行．
练习册系列答案
相关题目
【题目】某研究机构对中学生记忆能力x和识图能力y进行统计分析，得到如下数据：
记忆能力x | 4 | 6 | 8 | 10 |
识图能力y | 3 | ﹡﹡﹡ | 6 | 8 |
由于某些原因，识图能力的一个数据丢失，但已知识图能力样本平均值是5.5．
（Ⅰ）求丢失的数据；
（Ⅱ）经过分析，知道记忆能力x和识图能力y之间具有线性相关关系，请用最小二乘法求出y关于x的线性回归方程 
；
（III）若某一学生记忆能力值为12，请你预测他的识图能力值．
