题目内容
如图,在三棱锥中S-ABC中,平面SAB⊥平面SBC,AB⊥BC,AS=AB.过A作AF⊥SB,垂足为F,点E,G分别是棱SA,SC的中点.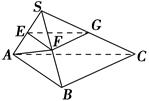
求证:(1)平面EFG∥平面ABC;
(2)BC⊥SA.
见解析
解析证明 (1)由AS=AB,AF⊥SB知F为SB中点,则EF∥AB,FG∥BC,又EF∩FG=F,因此平面EFG∥平面ABC.
(2)由平面SAB⊥平面SBC,且AF⊥SB,知AF⊥平面SBC,则AF⊥BC.
又BC⊥AB,AF∩AB=A,则BC⊥平面SAB,因此BC⊥SA.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
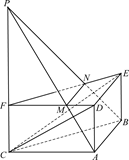
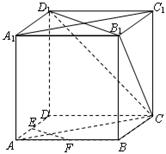
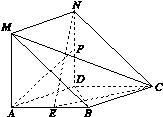
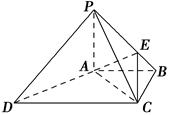
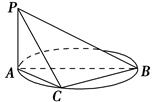
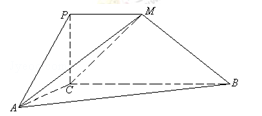
 为直角梯形,
为直角梯形,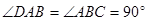 ,
, 平面
平面
 平面
平面 ;
;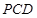 所成锐二面角的余弦值.
所成锐二面角的余弦值.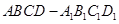 中,E为
中,E为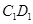 的中点.
的中点.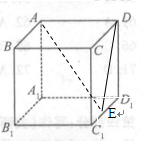
 ;
; 所成的角的正弦值.
所成的角的正弦值.