题目内容
【题目】下列命题中,正确的命题是( )
A.若a>b,c>d,则ac>bdB.若![]() ,则 a<b
,则 a<b
C.若b>c,则|a|b≥|a|cD.若a>b,c>d,则a﹣c>b﹣d
【答案】C
【解析】
直接根据不等式的基本性质对各选项做出判断,主要是不等式的“同向相乘”和“同向相加”的性质,注意前提条件.
根据不等式的基本性质,依次判断选项:
对于A选项:只有当a>b>0,c>d>0,才能推得ac>bd,所以A选项不合题意;
对于B选项:只有当ab>0时,才能由![]() 推得a<b,所以B选项不合题意;
推得a<b,所以B选项不合题意;
对于C选项:需要分类讨论如下:
①当a=0时,不等式两边都为零,式子成立,
②当a≠0时,|a|≠0,由b>c,可推得|a|b>|a|c,所以C选项符合题意;
对于D选项:该式不等式,由a>b,c>d不能“同向相减”得出a﹣c>b﹣d,
但是可以运用同向相加得到,a﹣d>b﹣c,因此,D选项不合题意.
故选C.

 走进文言文系列答案
走进文言文系列答案【题目】随着人民生活水平的日益提高,某小区居民拥有私家车的数量与日俱增.由于该小区建成时间较早,没有配套建造地下停车场,小区内无序停放的车辆造成了交通的拥堵.该小区的物业公司统计了近五年小区登记在册的私家车数量(累计值,如147表示2016年小区登记在册的所有车辆数,其余意义相同),得到如下数据:
编号 | 1 | 2 | 3 | 4 | 5 |
年份 | 2014 | 2015 | 2016 | 2017 | 2018 |
数量 | 37 | 104 | 147 | 196 | 216 |
(1)若私家车的数量![]() 与年份编号
与年份编号![]() 满足线性相关关系,求
满足线性相关关系,求![]() 关于
关于![]() 的线性回归方程,并预测2020年该小区的私家车数量;
的线性回归方程,并预测2020年该小区的私家车数量;
(2)小区于2018年底完成了基础设施改造,划设了120个停车位.为解决小区车辆乱停乱放的问题,加强小区管理,物业公司决定禁止无车位的车辆进入小区.由于车位有限,物业公司决定在2019年度采用网络竞拍的方式将车位对业主出租,租期一年,竞拍方案如下:①截至2018年己登记在册的私家车业主拥有竞拍资格;②每车至多中请一个车位,由车主在竞拍网站上提出申请并给出自己的报价;③根据物价部门的规定,竞价不得超过1200元;④申请阶段截止后,将所有申请的业主报价自高到低排列,排在前120位的业主以其报价成交;⑤若最后出现并列的报价,则以提出申请的时间在前的业主成交,为预测本次竞拍的成交最低价,物业公司随机抽取了有竞拍资格的40位业主,进行了竞拍意向的调查,并对他们的拟报竞价进行了统计,得到如图频率分布直方图:
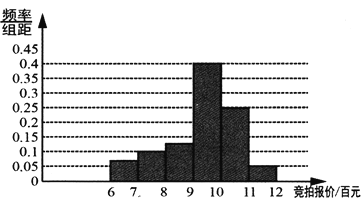
(i)求所抽取的业主中有意向竞拍报价不低于1000元的人数;
(ii)如果所有符合条件的车主均参与竞拍,利用样本估计总体的思想,请你据此预测至少需要报价多少元才能竞拍车位成功?(精确到整数)
参考公式及数据:对于一组数据![]() ,其回归方程
,其回归方程![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: ;
;![]() .
.
【题目】《朗读者》是一档文化情感类节目,以个人成长、情感体验、背景故事与传世佳作相结合的方式,选用精美的文字,用最平实的情感读出文字背后的价值,深受人们的喜爱.为了了解人们对该节目的喜爱程度,某调查机构随机调查了![]() ,
,![]() 两个城市各100名观众,得到下面的列联表.
两个城市各100名观众,得到下面的列联表.
非常喜爱 | 喜爱 | 合计 | |
| 60 | 100 | |
| 30 | ||
合计 | 200 |
完成上表,并根据以上数据,判断是否有![]() 的把握认为观众的喜爱程度与所处的城市有关?
的把握认为观众的喜爱程度与所处的城市有关?
附参考公式和数据: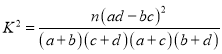 (其中
(其中![]() ).
).
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |