题目内容
13. 已知函数f(x)=sin(ωx+$\frac{π}{6}$)(ω>0,x∈R)的最小正周期为π.
已知函数f(x)=sin(ωx+$\frac{π}{6}$)(ω>0,x∈R)的最小正周期为π.(1)求ω的值;
(2)在给定的平面直角坐标系中,画出函数f(x)在区间[0,π]上的图象;
(3)求函数f(x)的最大值,并写出使函数f(x)取得最大值的x的集合.
分析 (1)由条件根据正弦函数周期性求得ω的值.
(2)由条件利用五点法作出函数f(x)在区间[0,π]上的图象.
(3)根据正弦函数的值域并结合f(x)的图象求得f(x)在区间[0,π]上的最大值以及f(x)取得最大值的x的集合.
解答 解:(1)∵函数f(x)=sin(ωx+$\frac{π}{6}$)(ω>0,x∈R)的最小正周期为π,∴$\frac{2π}{ω}$=π,∴ω=2.
(2)由x∈[0,π],可得2x+$\frac{π}{6}$∈间[$\frac{π}{6}$,$\frac{13π}{6}$],列表如下:
| 2x+$\frac{π}{6}$ | $\frac{π}{6}$ | $\frac{π}{2}$ | π | $\frac{3π}{2}$ | 2π | $\frac{13π}{6}$ |
| x | 0 | $\frac{π}{6}$ | $\frac{5π}{12}$ | $\frac{2π}{3}$ | $\frac{11π}{12}$ | π |
| y | $\frac{1}{2}$ | 1 | 0 | -1 | 0 |
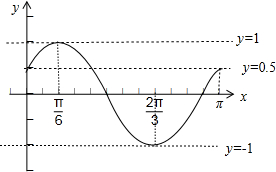
(3)当2x+$\frac{π}{6}$=2kπ+$\frac{π}{2}$,k∈z时,即x=kπ+$\frac{π}{6}$,k∈z时,函数f(x)取得最大值为1.
点评 本题主要考查由函数y=Asin(ωx+φ)的部分图象求解析式,用五点法作函数在一个周期上的简图,正弦函数周期性和的值域,属于中档题.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
8.对于集合M,定义函数fM(x)=$\left\{\begin{array}{l}{-1,x∈M}\\{1,x∉M}\end{array}\right.$,对于两个集合M、N,定义集合M⊕N={x|fM(x)•fN(x)=-1},已知A={2,4,6,8,10},B={1,2,4,5,6,8,9},则集合A⊕B=( )
| A. | {1,5,9,10} | B. | {1,5,9} | C. | {2,4,6} | D. | {2,4,6,8} |
5.已知a∈R,复数i2-ai在复平面内对应的点在直线x-y=0上,则实数a的值是( )
| A. | 1 | B. | 0 | C. | -1 | D. | 2 |
 设b>0,椭圆方程为$\frac{{x}^{2}}{2{b}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1,抛物线方程为y=$\frac{1}{8}$x2+b,如图所示,过点F(0,b+2)作x轴的平行线,与抛物线在第一象限的焦点为G,已知抛物线在G点的切线经过椭圆的右焦点F1
设b>0,椭圆方程为$\frac{{x}^{2}}{2{b}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1,抛物线方程为y=$\frac{1}{8}$x2+b,如图所示,过点F(0,b+2)作x轴的平行线,与抛物线在第一象限的焦点为G,已知抛物线在G点的切线经过椭圆的右焦点F1