题目内容
3.已知函数f(x)=x2+bx+c,其中0≤b≤4,0≤c≤4,记函数f(x)满足条件$\left\{\begin{array}{l}{f(2)≤12}\\{f(-2)≤4}\end{array}\right.$为事件为A,则事件A发生的概率为$\frac{1}{2}$.分析 我们可以以b,c为横纵坐标建立坐标系,并把0≤b≤4,0≤c≤4所表示的区域表示出来,并将$\left\{\begin{array}{l}{f(2)≤12}\\{f(-2)≤4}\end{array}\right.$代入函数f(x)=x2+bx+x转化为一个关于b、c的不等式,画出其表示的图形,计算面积后,代入几何概型公式,即可求解.
解答 解:$\left\{\begin{array}{l}{f(2)≤12}\\{f(-2)≤4}\end{array}\right.$即$\left\{\begin{array}{l}{4+2b+c≤12}\\{4-2b+c≤4}\end{array}\right.$.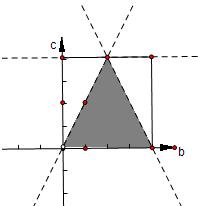
以b,c为横纵坐标建立坐标系如图:
所以满足条件的概率为$\frac{1}{2}$.
故答案为:$\frac{1}{2}$
点评 几何概型的概率估算公式中的“几何度量”,可以为线段长度、面积、体积等,而且这个“几何度量”只与“大小”有关,而与形状和位置无关.

练习册系列答案
相关题目
18.已知集合A={0,1,2,3},集合B={x|x2≤4},则A∩B=( )
| A. | {3} | B. | {1,2} | C. | {0,1,2} | D. | {0,1,2,3} |
8.设复数z满足z•(1-i)=2,则复数z的模|z|等于( )
| A. | 1 | B. | 4 | C. | 2 | D. | $\sqrt{2}$ |
 已知函数f(x)=sin(ωx+$\frac{π}{6}$)(ω>0,x∈R)的最小正周期为π.
已知函数f(x)=sin(ωx+$\frac{π}{6}$)(ω>0,x∈R)的最小正周期为π. 如图,四边形ABCD为矩形,AD⊥平面ABE,AE=EB=BC=2,F为CE上的点,且BF⊥平面ACE,
如图,四边形ABCD为矩形,AD⊥平面ABE,AE=EB=BC=2,F为CE上的点,且BF⊥平面ACE, 已知:过抛物线x2=4y的焦点F的直线交抛物线于A,B两个不同的点,过A,B分别作抛物线的切线,且二者相交于点C.
已知:过抛物线x2=4y的焦点F的直线交抛物线于A,B两个不同的点,过A,B分别作抛物线的切线,且二者相交于点C.