题目内容
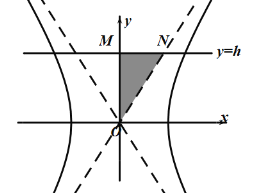
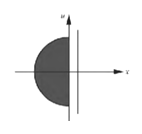
【题目】关于旋转体的体积，有如下的古尔丁（guldin）定理：“平面上一区域D绕区域外一直线（区域D的每个点在直线的同侧，含直线上）旋转一周所得的旋转体的体积，等于D的面积与D的几何中心（也称为重心）所经过的路程的乘积”．利用这一定理，可求得半圆盘
，绕直线x
旋转一周所形成的空间图形的体积为_____．
【答案】2π
【解析】
显然半圆的几何中心在半圆与x轴的交线上，设几何中心到原点的距离为x，根据古尔丁（guldin）定理求得球的体积，根据球的体积公式列等式可解得
，再根据这一定理即可求得结果.
显然半圆的几何中心在半圆与x轴的交线上，设几何中心到原点的距离为x，
则由题意得：2πx（
）
，解得x
，
所以几何中心到直线x
的距离为：
，
所以得到的几何体的体积为：V＝（2π
）（）＝2π．
故答案为：
练习册系列答案
相关题目
