题目内容
【题目】已知双曲线![]() 的渐近线方程为
的渐近线方程为![]() ,一个焦点为
,一个焦点为![]() .
.
(1)求双曲线![]() 的方程;
的方程;
(2)过双曲线![]() 上的任意一点
上的任意一点![]() ,分别作这两条渐近线的平行线与这两条渐近线得到四边形
,分别作这两条渐近线的平行线与这两条渐近线得到四边形![]() ,证明四边形
,证明四边形![]() 的面积是一个定值;
的面积是一个定值;
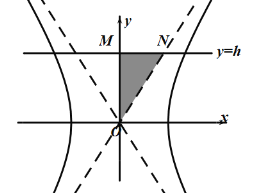
(3)设直线![]() 与
与![]()
![]() 在第一象限内与渐近线
在第一象限内与渐近线![]() 所围成的三角形
所围成的三角形![]() 绕着
绕着![]() 轴旋转一周所得几何体的体积.
轴旋转一周所得几何体的体积.
【答案】(1)![]() ;(2)证明见解析;(3)
;(2)证明见解析;(3)![]()
【解析】
(1)由焦点坐标和渐近线方程求得![]() ,进而求得双曲线方程;
,进而求得双曲线方程;
(2)由题可知渐近线互相垂直,则四边形![]() 为矩形,则
为矩形,则![]() ,利用点到直线距离公式求解即可;
,利用点到直线距离公式求解即可;
(3)三角形![]() 绕着
绕着![]() 轴旋转一周所得几何体是一个以
轴旋转一周所得几何体是一个以![]() 为半径,
为半径,![]() 为高的圆锥,进而求解即可
为高的圆锥,进而求解即可
解:(1)设双曲线方程为![]()
![]() ,
,
![]()
![]() ,渐近线方程为
,渐近线方程为![]() ,
,
![]()
![]() ,且
,且![]() ,
,
![]() ,
,
双曲线![]() 的方程为
的方程为![]()
(2)![]() 渐近线方程为
渐近线方程为![]() ,
,
![]() 两条渐近线互相垂直,
两条渐近线互相垂直,
![]() 四边形
四边形![]() 为矩形,
为矩形,
设![]() ,则
,则![]() ,
,
![]()
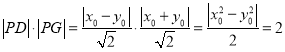 ,
,
![]() 四边形
四边形![]() 的面积是一个定值
的面积是一个定值
(3)设![]() 在第一象限内与渐近线的交点N的横坐标
在第一象限内与渐近线的交点N的横坐标![]() ,三角形
,三角形![]() 绕着
绕着![]() 轴旋转一周所得几何体是一个以
轴旋转一周所得几何体是一个以![]() 为半径,
为半径,![]() 为高的圆锥,
为高的圆锥,
因为![]() ,所以体积等于
,所以体积等于![]()

练习册系列答案
相关题目
【题目】某网络营销部门为了统计某市网友某日在某淘宝店的网购情况,随机抽查了该市当天![]() 名网友的网购金额情况,得到如下统计表(如图).
名网友的网购金额情况,得到如下统计表(如图).
网购金额(单位:千元) | 频数 | 频率 |
| 3 | 0.05 |
|
|
|
| 9 | 0.15 |
| 15 | 0.25 |
| 18 | 0.30 |
|
|
|

若网购金额超过![]() 千元的顾客定义为“网购达人”,网购金额不超过
千元的顾客定义为“网购达人”,网购金额不超过![]() 千元的顾客定义为“非网购达人”,已知“非网购达人”与“网购达人”人数比恰好为
千元的顾客定义为“非网购达人”,已知“非网购达人”与“网购达人”人数比恰好为![]() .
.
(Ⅰ)试确定![]() 的值,并补全频率分布直方图(如图);
的值,并补全频率分布直方图(如图);
(Ⅱ)该营销部门为了进一步了解这![]() 名网友的购物体验,从“非网购达人”与“网购达人”中用分层抽样的方法抽取
名网友的购物体验,从“非网购达人”与“网购达人”中用分层抽样的方法抽取![]() 人,若需从这
人,若需从这![]() 人中随机选取
人中随机选取![]() 人进行问卷调查.设
人进行问卷调查.设![]() 为选取的
为选取的![]() 人中“网购达人”的人数,求
人中“网购达人”的人数,求![]() 的分布列及其数学期望.
的分布列及其数学期望.