题目内容
【题目】过△ABC所在平面α外一点P，作PO⊥α，垂足为O，连接PA，PB，PC，若点O是△ABC的内心，则（ ）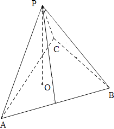
A.PA=PB=PC
B.点P到AB，BC，AC的距离相等
C.PA⊥PB，PB⊥PC，PC⊥PA
D.PA，PB，PC与平面α所成的角相等
【答案】B
【解析】解：过O做三角形ABC三边的高，垂足分别为D，E，F，连接PD，PE，PF，如图所示：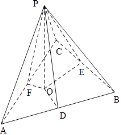
∵O是△ABC的内心，
∴OD=OE=OF，
∵PO⊥平面α，OD平面α，OE平面α，OF平面α，
∴PO⊥OD，PO⊥OE，PO⊥OF，
∴Rt△POD=Rt△POE=RtPOF，
∴PD=PE=PF，
∵AB⊥OD，AB⊥PO，
∴AB⊥平面POD，
∴AB⊥PD，即PD为P到AB的距离，
同理PE⊥BC，PF⊥AC，
∴点P到AB，BC，AC的距离相等．
故选B．
练习册系列答案
相关题目
