题目内容
9.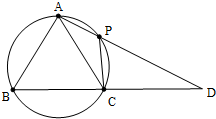 在△ABC中,AB=AC,过点A的直线与其外接圆交于点P,交BC延长线于点D.
在△ABC中,AB=AC,过点A的直线与其外接圆交于点P,交BC延长线于点D.(Ⅰ)求证:$\frac{PC}{AC}=\frac{PD}{BD}$;
(Ⅱ)若AC=2,求AP•AD的值.
分析 (Ⅰ)证明:△DPC∽△DBA,即可证明$\frac{PC}{AC}=\frac{PD}{BD}$;
(Ⅱ)证明△APC∽△ACD,即可求AP•AD的值.
解答 (Ⅰ)证明:∵∠CPD=∠ABC,∠D=∠D,
∴△DPC∽△DBA.
∴$\frac{PC}{AB}=\frac{PD}{BD}$.
又∵AB=AC,∴$\frac{PC}{AC}=\frac{PD}{BD}$…(5分)
(Ⅱ)解:∵∠ACD=∠APC,∠CAP=∠CAD,∴△APC∽△ACD.
∴$\frac{AP}{AC}=\frac{AC}{AD}$,∴AC2=AP•AD=4…(10分)
点评 本题考查三角形相似的性质与判定,考查学生分析解决问题的能力,比较基础.

练习册系列答案
相关题目
19.将y=2cos($\frac{x}{3}$+$\frac{π}{6}$)图象按向量$\overrightarrow{a}$=(-$\frac{π}{4}$,-2)平移,则平移后所得函数的周期及图象的一个对称中心分别为( )
| A. | 3π,$({\frac{π}{4},-2})$ | B. | 6π,$({\frac{3π}{4},2})$ | C. | 6π,$({\frac{3π}{4},-2})$ | D. | 3π,$({\frac{π}{4},2})$ |
4.已知△ABC是非等腰三角形,设P(cosA,sinA),Q(cosB,sinB),R(cosC,sinC),则△PQR的形状是( )
| A. | 锐角三角形 | B. | 钝角三角形 | C. | 直角三角形 | D. | 不确定 |
18.已知抛物线y2=4x,过其焦点F作倾斜角为$\frac{π}{4}$的直线l,若l与抛物线交于B、C两点,则弦BC的长为( )
| A. | $\frac{10}{3}$ | B. | 2 | C. | 4 | D. | 8 |
 如图,四棱锥P-ABCD的底面ABCD是平行四边形,M,N分别为PB,CD的中点,二面角P-CD-A的大小为60°,AC=AD=$\sqrt{2}$,CD=PN=2,PC=PD.
如图,四棱锥P-ABCD的底面ABCD是平行四边形,M,N分别为PB,CD的中点,二面角P-CD-A的大小为60°,AC=AD=$\sqrt{2}$,CD=PN=2,PC=PD. 如图:在三棱锥P-ABC中,AB=AC=2$\sqrt{10}$,BC=4,PC=2$\sqrt{11}$,点P在平面ABC内的射影恰为△ABC的重心G,M为侧棱AP上一动点.
如图:在三棱锥P-ABC中,AB=AC=2$\sqrt{10}$,BC=4,PC=2$\sqrt{11}$,点P在平面ABC内的射影恰为△ABC的重心G,M为侧棱AP上一动点.