题目内容
1.已知角α的顶点与原点重合,始边与x轴的正半轴重合,终边与单位圆的交点坐标为($\frac{3\sqrt{10}}{10}$,$\frac{\sqrt{10}}{10}$),则cos2α=$\frac{4}{5}$.分析 先求得sinα和cosα的值,进而利用余弦的二倍角公式求得答案.
解答 解:依题意可知sinα=$\frac{\sqrt{10}}{10}$,cosα$\frac{3\sqrt{10}}{10}$,
∴cos2α=cos2α-sin2α=$\frac{9}{10}$-$\frac{1}{10}$=$\frac{4}{5}$,
故答案为:$\frac{4}{5}$.
点评 本题主要考查了二倍角的余弦公式,考查了学生对基础公式的熟练记忆.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
12.函数f(x)=(x-a)ex在区间(2,3)内没有极值点,则实数a的取值范围是( )
| A. | (-∞,3]∪[4,+∞) | B. | [3,4] | C. | (-∞,3] | D. | [4,+∞) |
16.设复数z=-1-i(i为虚数单位),则$\frac{2-\overline{z}}{z}$对应的点位于( )
| A. | 第四象限 | B. | 第三象限 | C. | 第二象限 | D. | 第一象限 |
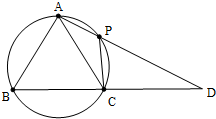 在△ABC中,AB=AC,过点A的直线与其外接圆交于点P,交BC延长线于点D.
在△ABC中,AB=AC,过点A的直线与其外接圆交于点P,交BC延长线于点D. 如图1,在Rt△ACB中,∠C=90°,BC=3,AC=6,D,E分别是AC,AB上的点,且DE∥BC,DE=2,将△ADE沿DE折起到△A1DE的位置.
如图1,在Rt△ACB中,∠C=90°,BC=3,AC=6,D,E分别是AC,AB上的点,且DE∥BC,DE=2,将△ADE沿DE折起到△A1DE的位置. A,B两名学生在5次英语口语测试中的成绩统计如茎叶图所示(十位作为茎).
A,B两名学生在5次英语口语测试中的成绩统计如茎叶图所示(十位作为茎).