题目内容
4.已知△ABC是非等腰三角形,设P(cosA,sinA),Q(cosB,sinB),R(cosC,sinC),则△PQR的形状是( )| A. | 锐角三角形 | B. | 钝角三角形 | C. | 直角三角形 | D. | 不确定 |
分析 根据两点间的距离公式求出对应的线段长度即可得到结论.
解答 解:易知这三个点都在单位圆上,而且都在第一,二象限,
由平几知识可知,这样的三个点构成的必然是钝角三角形.
故选:B.
点评 本题主要考查三角形形状的判断,根据两点间的距离公式是解决本题的关键.

练习册系列答案
相关题目
14.将6名留学归国人员分配到济南、青岛两地工作.若济南至少安排2 人,青岛至少安排3人,则不同的安排方法数为( )
| A. | 120 | B. | 150 | C. | 35 | D. | 55 |
12.函数f(x)=(x-a)ex在区间(2,3)内没有极值点,则实数a的取值范围是( )
| A. | (-∞,3]∪[4,+∞) | B. | [3,4] | C. | (-∞,3] | D. | [4,+∞) |
19.已知集合A={x|-1<x<1},B={x|x2-3x≤0},则A∩B等于( )
| A. | [-1,0] | B. | (-1,3] | C. | [0,1) | D. | {-1,3} |
16.设复数z=-1-i(i为虚数单位),则$\frac{2-\overline{z}}{z}$对应的点位于( )
| A. | 第四象限 | B. | 第三象限 | C. | 第二象限 | D. | 第一象限 |
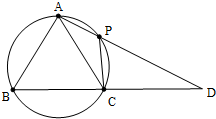 在△ABC中,AB=AC,过点A的直线与其外接圆交于点P,交BC延长线于点D.
在△ABC中,AB=AC,过点A的直线与其外接圆交于点P,交BC延长线于点D. 如图1,在Rt△ACB中,∠C=90°,BC=3,AC=6,D,E分别是AC,AB上的点,且DE∥BC,DE=2,将△ADE沿DE折起到△A1DE的位置.
如图1,在Rt△ACB中,∠C=90°,BC=3,AC=6,D,E分别是AC,AB上的点,且DE∥BC,DE=2,将△ADE沿DE折起到△A1DE的位置.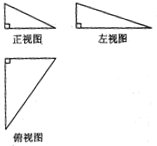 一个三棱锥的三视图如图所示,其正视图、左视图、俯视图的面积分别是1,2,4,则这个几何体的外接球的表面积为21π.
一个三棱锥的三视图如图所示,其正视图、左视图、俯视图的面积分别是1,2,4,则这个几何体的外接球的表面积为21π.