题目内容
已知定义在R上的函数y=f(x)满足以下三个条件:①对于任意的x∈R,都有f(x+4)=f(x);②对于任意的x1,x2∈R,且0≤x1<x2≤2,都有f(x1)<f(x2);③函数y=f(x+2)的图象关于y轴对称.则下列结论中正确的是( ).
| A.f(4.5)<f(7)<f(6.5) | B.f(7)<f(4.5)<f(6.5) |
| C.f(7)<f(6.5)<f(4.5) | D.f(4.5)<f(6.5)<f(7) |
A
由已知得f(x)是以4为周期且关于直线x=2对称的函数.∴f(4.5)=f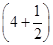 =f
=f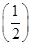 ,f(7)=f(4+3)=f(3)=f(1),
,f(7)=f(4+3)=f(3)=f(1),
f(6.5)=f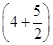 =f
=f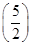 =f
=f .
.
又f(x)在[0,2]上为增函数.故有所以f >f(1)>f
>f(1)>f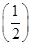 ,f(4.5)<f(7)<f(6.5).
,f(4.5)<f(7)<f(6.5).
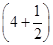 =f
=f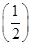 ,f(7)=f(4+3)=f(3)=f(1),
,f(7)=f(4+3)=f(3)=f(1),f(6.5)=f
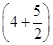 =f
=f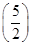 =f
=f .
.又f(x)在[0,2]上为增函数.故有所以f
 >f(1)>f
>f(1)>f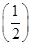 ,f(4.5)<f(7)<f(6.5).
,f(4.5)<f(7)<f(6.5).
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
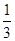 )=0,则不等式
)=0,则不等式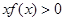 的解集是( )
的解集是( ) 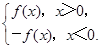 若f(-1)=0,且对任意实数x均有f(x)≥0成立.
若f(-1)=0,且对任意实数x均有f(x)≥0成立.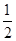 x2+4x-3ln x在[t,t+1]上不单调,则t的取值范围是______.
x2+4x-3ln x在[t,t+1]上不单调,则t的取值范围是______.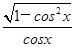 ( ).
( ). 上递增
上递增 上递增,在
上递增,在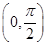 上递减
上递减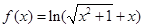 ,若实数
,若实数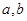 满足
满足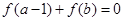 ,则
,则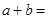 ______.
______.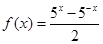 ( )
( ) 上是减函数
上是减函数 ,对于给定的正数
,对于给定的正数 ,定义函数
,定义函数 若对于函数
若对于函数 ,恒有
,恒有 ,则( )
,则( )