题目内容
已知二次函数f(x)=ax2+bx+1(a>0),F(x)=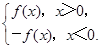 若f(-1)=0,且对任意实数x均有f(x)≥0成立.
若f(-1)=0,且对任意实数x均有f(x)≥0成立.
(1)求F(x)的表达式;
(2)当x∈[-2,2]时,g(x)=f(x)-kx是单调函数,求k的取值范围.
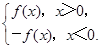 若f(-1)=0,且对任意实数x均有f(x)≥0成立.
若f(-1)=0,且对任意实数x均有f(x)≥0成立.(1)求F(x)的表达式;
(2)当x∈[-2,2]时,g(x)=f(x)-kx是单调函数,求k的取值范围.
(1)F(x)=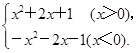 (2)(-∞,-2]∪[6,+∞)
(2)(-∞,-2]∪[6,+∞)
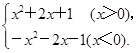 (2)(-∞,-2]∪[6,+∞)
(2)(-∞,-2]∪[6,+∞)(1)∵f(-1)=0,∴a-b+1=0,∴b=a+1,
∴f(x)=ax2+(a+1)x+1.
∵f(x)≥0恒成立,
∴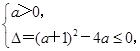 即
即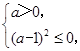
∴a=1,从而b=2,∴f(x)=x2+2x+1,
∴F(x)=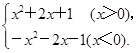
(2)由(1)知,g(x)=x2+2x+1-kx=x2+(2-k)x+1.
∵g(x)在[-2,2]上是单调函数,
∴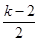 ≤-2或
≤-2或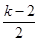 ≥2,
≥2,
解得k≤-2或k≥6.
所以k的取值范围是(-∞,-2]∪[6,+∞)
∴f(x)=ax2+(a+1)x+1.
∵f(x)≥0恒成立,
∴
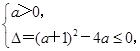 即
即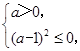
∴a=1,从而b=2,∴f(x)=x2+2x+1,
∴F(x)=
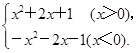
(2)由(1)知,g(x)=x2+2x+1-kx=x2+(2-k)x+1.
∵g(x)在[-2,2]上是单调函数,
∴
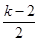 ≤-2或
≤-2或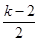 ≥2,
≥2,解得k≤-2或k≥6.
所以k的取值范围是(-∞,-2]∪[6,+∞)

练习册系列答案
相关题目
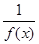 的单调区间表述正确的是( )
的单调区间表述正确的是( )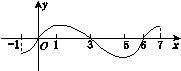
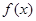 为定义在
为定义在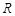 上的偶函数,当
上的偶函数,当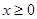 时,有
时,有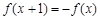 ,且当
,且当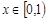 时,
时,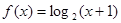 ,给出下列命题:
,给出下列命题: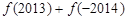 的值为0;②函数
的值为0;②函数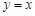 与函数
与函数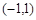 .
.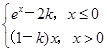 是R上的增函数,则实数k的取值范围是________.
是R上的增函数,则实数k的取值范围是________.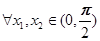 ,若
,若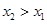 ,且
,且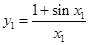 ,
,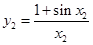 ,则( )
,则( )