题目内容
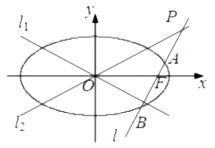
【题目】如图所示,已知椭圆![]() 的焦距为
的焦距为 ![]() ,直线
,直线![]() 被椭圆
被椭圆 ![]() 截得的弦长为
截得的弦长为![]() .
.

(1)求椭圆 ![]() 的方程;
的方程;
(2)设点![]() 是椭圆
是椭圆 ![]() 上的动点,过原点
上的动点,过原点![]() 引两条射线
引两条射线![]() 与圆
与圆![]() 分别相切,且
分别相切,且![]() 的斜率
的斜率![]() 存在. ①试问
存在. ①试问 ![]() 是否为定值?若是,求出该定值,若不是,说明理由;
是否为定值?若是,求出该定值,若不是,说明理由;
②若射线![]() 与椭圆
与椭圆 ![]() 分别交于点
分别交于点![]() ,求
,求![]() 的最大值.
的最大值.
【答案】(1)![]() ;(2)①
;(2)①![]() ,②
,②![]() .
.
【解析】试题分析:(1)利用题意求出点![]() 的坐标,将点
的坐标,将点![]() 的坐标代入椭圆方程,进而求出椭圆的标准方程;(2)①设出射线方程,利用直线和圆相切得到有关关系式,再结合点在椭圆上进行证明;②联立直线和椭圆方程,得到相关点的坐标,再利用基本不等式求其最值.
的坐标代入椭圆方程,进而求出椭圆的标准方程;(2)①设出射线方程,利用直线和圆相切得到有关关系式,再结合点在椭圆上进行证明;②联立直线和椭圆方程,得到相关点的坐标,再利用基本不等式求其最值.
试题解析: (1) 依题意得![]() ,设直线
,设直线 ![]() 与椭圆
与椭圆 ![]() 相交于
相交于 ![]() 两点,则
两点,则![]() ,不妨设
,不妨设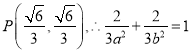 ,又
,又![]() ,解得
,解得![]() ,所以椭圆
,所以椭圆 ![]() 的方程为
的方程为![]() .
.
(2) ①设射线![]() 方程为
方程为![]() ,则
,则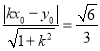 ,两边平方整理得
,两边平方整理得![]() ,
, 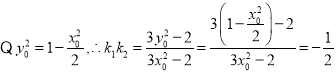 .
.
②联立![]() ,消去
,消去 ![]() 得
得![]() ,同理
,同理![]() ,
, 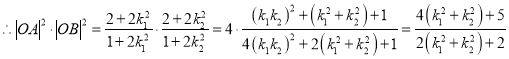
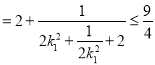 ,当且仅当
,当且仅当![]() 时,取等号
时,取等号![]() .
.

【题目】某农场计划种植某种新作物,为此对这种作物的两个品种(分别称为品种甲和品种乙)进行田间试验.选取两大块地,每大块地分成![]() 小块地,在总共
小块地,在总共![]() 小块地中,随机选
小块地中,随机选![]() 小块地种植品种甲,另外
小块地种植品种甲,另外![]() 小块地种植品种乙.
小块地种植品种乙.
(1)假设![]() ,求第一大块地都种植品种甲的概率;
,求第一大块地都种植品种甲的概率;
(2)试验时每大块地分成![]() 小块,即
小块,即![]() ,试验结束后得到品种甲和品种乙在各小块地上的每公顷产量(单位:kg/hm2)如下表:
,试验结束后得到品种甲和品种乙在各小块地上的每公顷产量(单位:kg/hm2)如下表:
甲 |
|
|
|
|
|
|
|
|
乙 |
|
|
|
|
|
|
|
|
分别求品种甲和品种乙的每公顷产量的样本平均数和样本方差;根据试验结果,你认为应该种植哪一品种?
【题目】孝感市及周边地区的市民游玩又添新去处啦!孝感熙凤水乡旅游度假区于2017年10月1日正式对外开放.据统计,从2017年10月1日到10月7日参观孝感市熙凤水乡旅游度假区的人数如表所示:
日期 | 1日 | 2日 | 3日 | 4日 | 5日 | 6日 | 7日 |
人数(万) | 11 | 13 | 8 | 9 | 7 | 8 | 10 |
(1)把这7天的参观人数看成一个总体,求该总体的众数和平均数(精确到0.1);
(2)用简单随机抽样方法从10月1日到10月4日中抽取2天,它们的参观人数组成一个样本,求该样本平均数与总体平均数之差的绝对值不超过1万的概率.