题目内容
【题目】已知椭圆![]() :
: ![]() ,设直线
,设直线![]() 与椭圆
与椭圆![]() 交于不同两点
交于不同两点![]() ,且
,且![]() .若点
.若点![]() 满足
满足![]() ,则
,则![]() =______________.
=______________.
【答案】![]() 或
或![]()
【解析】由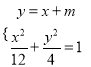 ,得
,得![]() ①
①
∵直线l与椭圆C交于不同两点![]() ,
,
∴![]() 得
得![]() <16.
<16.
设![]() 则
则![]() ,
,![]() 是方程①的两根,
是方程①的两根,
则![]() .
.
∴![]() .
.
又由![]() ,得
,得![]() ,解之m=±2.
,解之m=±2.
据题意知,点P为线段AB的中垂线与直线y=2的交点。
设AB的中点为![]() ,则
,则![]() ,
,
当m=2时, ![]() .
.
∴此时,线段AB的中垂线方程为![]() ,即y=x1.
,即y=x1.
令y=2,得![]() =3.
=3.
当m=2时,E(![]() ,
,![]() ).
).
∴此时,线段AB的中垂线方程为![]() ,即y=x+1.
,即y=x+1.
令y=2,得![]() =1.
=1.
综上所述, ![]() 的值为3或1.
的值为3或1.
点睛: 本题主要考查直线与圆锥曲线位置关系,所使用方法为韦达定理法:因直线的方程是一次的,圆锥曲线的方程是二次的,故直线与圆锥曲线的问题常转化为方程组关系问题,最终转化为一元二次方程问题,故用韦达定理及判别式是解决圆锥曲线问题的重点方法之一,尤其是弦中点问题,弦长问题,可用韦达定理直接解决,但应注意不要忽视判别式的作用.

练习册系列答案
相关题目

