题目内容
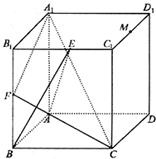 如图,在正方体ABCD-A1B1C1D1中,E、F、M分别是棱B1C1、B1B1、C1D1的中点.
如图,在正方体ABCD-A1B1C1D1中,E、F、M分别是棱B1C1、B1B1、C1D1的中点.(Ⅰ)求证:CF⊥平面EAB;
(Ⅱ)是否存在过E、M点且与平面A1FC平行的平面?若存在,请指出并证明之;若不存在,请说明
理由.
分析:(Ⅰ)欲证CF⊥平面EAB,可证CF⊥BE,CF⊥AB,其中CF⊥BE可由△BB1E≌△BCF得到∠B1BE=∠BCF,从而∠BCF+∠EBC=90°,根据线面垂直的判定定理进行判定即可;
(2)先找出符合题意的平面,然后进行证明,欲证平面EMN∥平面A1FC,根据面面平行的判定定理可知只需在一个平面内找两相交直线与另一平面平行,而EN∥平面A1FC,MN∥平面A1FC,EN∩MN=N,满足定理条件.
(2)先找出符合题意的平面,然后进行证明,欲证平面EMN∥平面A1FC,根据面面平行的判定定理可知只需在一个平面内找两相交直线与另一平面平行,而EN∥平面A1FC,MN∥平面A1FC,EN∩MN=N,满足定理条件.
解答: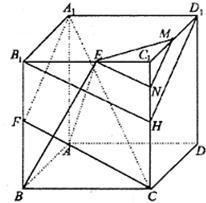 (I)证明:在正方形B1BCC1中,∵E、F分别为B1C1、B1B的中点,
(I)证明:在正方形B1BCC1中,∵E、F分别为B1C1、B1B的中点,
∴△BB1E≌△BCF,∴∠B1BE=∠BCF,
∴∠BCF+∠EBC=90°,∴CF⊥BE
又AB⊥平面B1BCC1,CF?平面B1BCC1,∴AB⊥CF,
又∵AB∩BE=B,∴CF⊥平面EAB.
(II)设N是棱C1C上的一点,且C1N=
C1C,
则平面EMN为符合要求的平面.
证明如下:
设H为棱C1C的中点,∵C1N=
C1C,
∴C1N=
C1H,又E为B1C1的中点,∴EN∥B1H,
又CF∥B1H,∴EN∥CF,∴EN∥平面A1FC
同理MN∥D1H,D1H∥A1F,
∴MN∥A1F,∴MN∥平面A1FC.
EN∩MN=N,∴平面EMN∥平面A1FC.
 (I)证明:在正方形B1BCC1中,∵E、F分别为B1C1、B1B的中点,
(I)证明:在正方形B1BCC1中,∵E、F分别为B1C1、B1B的中点,∴△BB1E≌△BCF,∴∠B1BE=∠BCF,
∴∠BCF+∠EBC=90°,∴CF⊥BE
又AB⊥平面B1BCC1,CF?平面B1BCC1,∴AB⊥CF,
又∵AB∩BE=B,∴CF⊥平面EAB.
(II)设N是棱C1C上的一点,且C1N=
| 1 |
| 4 |
则平面EMN为符合要求的平面.
证明如下:
设H为棱C1C的中点,∵C1N=
| 1 |
| 4 |
∴C1N=
| 1 |
| 2 |
又CF∥B1H,∴EN∥CF,∴EN∥平面A1FC
同理MN∥D1H,D1H∥A1F,
∴MN∥A1F,∴MN∥平面A1FC.
EN∩MN=N,∴平面EMN∥平面A1FC.
点评:本题主要考查了直线与平面垂直的判定,以及平面与平面平行的判定,这种题型是高考的趋势,属于基础题.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
 若Rt△ABC中两直角边为a、b,斜边c上的高为h,则
若Rt△ABC中两直角边为a、b,斜边c上的高为h,则 如图,在正方体的一角上截取三棱锥P-ABC,PO为棱锥的高,记
如图,在正方体的一角上截取三棱锥P-ABC,PO为棱锥的高,记 若Rt△ABC中两直角边为a、b,斜边c上的高为h,则
若Rt△ABC中两直角边为a、b,斜边c上的高为h,则 如图,在正方体ABCD-A1B1C1D1中,E为DD1的中点,
如图,在正方体ABCD-A1B1C1D1中,E为DD1的中点, 如图,在正方体ABCD-A1B1C1D1中,点P是上底面A1B1C1D1内一动点,则三棱锥P-ABC的主视图与左视图的面积的比值为( )
如图,在正方体ABCD-A1B1C1D1中,点P是上底面A1B1C1D1内一动点,则三棱锥P-ABC的主视图与左视图的面积的比值为( )