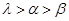题目内容
已知函数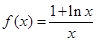

(1)求函数f(x)的极值;
(2)如果当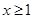 时,不等式
时,不等式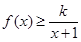 恒成立,求实数k的取值范围;
恒成立,求实数k的取值范围;
(3)求证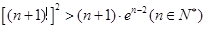 .
.
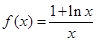

(1)求函数f(x)的极值;
(2)如果当
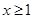 时,不等式
时,不等式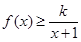 恒成立,求实数k的取值范围;
恒成立,求实数k的取值范围;(3)求证
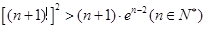 .
.(1)函数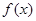 在
在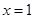 处取得极大值f(1)="1" ,无极小值。
处取得极大值f(1)="1" ,无极小值。
(2)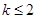
(3)见解析
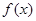 在
在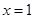 处取得极大值f(1)="1" ,无极小值。
处取得极大值f(1)="1" ,无极小值。(2)
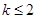
(3)见解析
试题分析:(1)利用导数的思想,通过导数的符号判定函数的单调性,进而得到极值。
(2)要证明不等式恒成立,移项,右边为零,将左边重新构造新的函数,证明函数的最小值大于零即可。
(3)在第二问的基础上,放缩法得到求和的不等式关系。
解:(1)因为

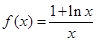 , x >0,则
, x >0,则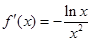 ,…………1分
,…………1分当
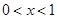 时,
时, ;当
;当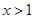 时,
时,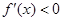 .
.所以
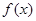 在(0,1)上单调递增;在
在(0,1)上单调递增;在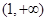 上单调递减,
上单调递减,所以函数
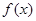 在
在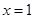 处取得极大值f(1)="1" ,无极小值。…………3分
处取得极大值f(1)="1" ,无极小值。…………3分(2)不等式
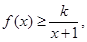 即为
即为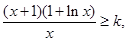 记
记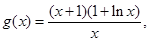
所以
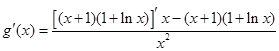
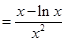 …………7分
…………7分令
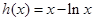 ,则
,则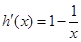 ,
, 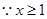 ,
, 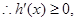
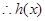 在
在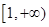 上单调递增,
上单调递增, 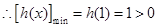 ,从而
,从而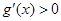 ,
,故
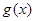 在
在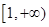 上也单调递增, 所以
上也单调递增, 所以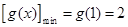 ,所以
,所以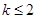 . ……9分
. ……9分(3)由(2)知:
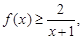 恒成立,即
恒成立,即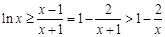 ,
, 令
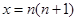 ,则
,则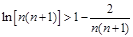
所以
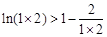 ,
, 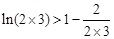 ,
, 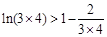 ,… …
,… … 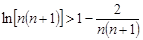 , …………12分
, …………12分叠加得:
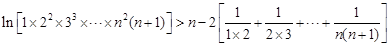
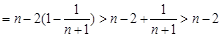 .
.则
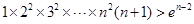 ,所以
,所以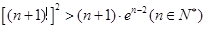 …………14分
…………14分点评:解决该试题的关键是对于导数的符号与函数单调性的熟练的运用,并能结合单调性求解函数的 极值和最值问题。难点是对于递进关系的试题,证明不等式,往往要用到上一问的结论。

练习册系列答案
相关题目
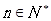 ,曲线
,曲线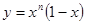 在
在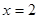 处的切线与
处的切线与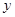 轴的交点的纵坐标为
轴的交点的纵坐标为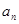 ,则
,则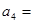 ( )
( ) .
.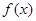 在
在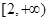 上是增函数,求实数
上是增函数,求实数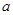 的取值范围;
的取值范围;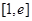 上的最小值为3,求实数
上的最小值为3,求实数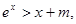 恒成立,则m的取值范围是 。
恒成立,则m的取值范围是 。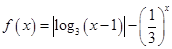 有两个零点
有两个零点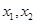 ,则( )
,则( )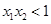
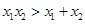
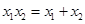
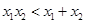
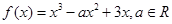
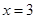 是
是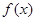 的极值点,求
的极值点,求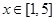 上的最大值
上的最大值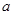 的取值范围.
的取值范围.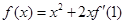 ,
,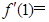 .
.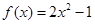 的图像上一点
的图像上一点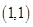 及邻近一点
及邻近一点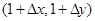 ,则
,则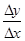 和
和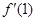 分别等于( )
分别等于( )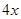 ,4
,4 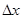 ,4
,4 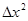 ,3
,3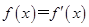 的较大实数根叫做函数
的较大实数根叫做函数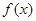 的“轻松点”,若函数
的“轻松点”,若函数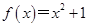 ,
,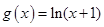 ,
,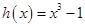 的“轻松点”分别为
的“轻松点”分别为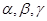 ,则
,则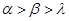 B.
B.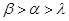 C.
C.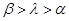 D.
D.