题目内容
【题目】已知椭圆![]() 的中心在坐标原点,焦点在
的中心在坐标原点,焦点在![]() 轴上,离心率
轴上,离心率![]() ,且椭圆
,且椭圆![]() 经过点
经过点![]() ,过椭圆
,过椭圆![]() 的左焦点
的左焦点![]() 且不与坐标轴垂直的直线交椭圆
且不与坐标轴垂直的直线交椭圆![]() 于
于![]() ,
,![]() 两点.
两点.
(1)求椭圆![]() 的方程;
的方程;
(2)设线段![]() 的垂直平分线与
的垂直平分线与![]() 轴交于点
轴交于点![]() ,求△
,求△![]() 的面积
的面积![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
试题分析:(1)根据椭圆的离心率![]() ,且椭圆
,且椭圆![]() 经过点
经过点![]() 列关于
列关于![]() 的方程组,解出
的方程组,解出![]() 的值,就可求得椭圆
的值,就可求得椭圆![]() 的方程;(2)设直线
的方程;(2)设直线![]() 的方程为
的方程为![]() (
(![]() ).由
).由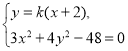 消去
消去![]() 并整理得
并整理得![]() ,先求得线段
,先求得线段![]() 的垂直平分线
的垂直平分线![]() 的方程,进而得
的方程,进而得![]()
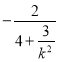
![]() ,进而
,进而![]() ,可得结果.
,可得结果.
试题解析:(1)设椭圆![]() 的方程为
的方程为![]() (
(![]() ),
),
则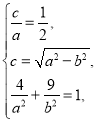 解得
解得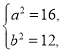
故椭圆![]() 的方程为
的方程为![]() .
.
(2)设直线![]() 的方程为
的方程为![]() (
(![]() ).
).
由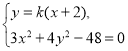 消去
消去![]() 并整理得
并整理得![]() .易知
.易知![]() ,
,
设![]() ,
,![]() ,则
,则![]() ,
,![]() ,
,
设![]() 是
是![]() 的中点,则
的中点,则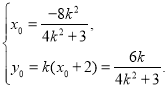
线段![]() 的垂直平分线
的垂直平分线![]() 的方程为
的方程为![]() ,
,
令![]() ,得
,得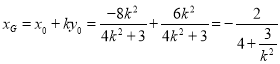 .
.
因为![]() ,所以
,所以![]() ,
,
因为![]() ,
,![]() ,
,
所以![]() 的取值范围是
的取值范围是![]() .
.

练习册系列答案
相关题目
【题目】某公司2016年前三个月的利润(单位:百万元)如下:
月份 |
|
|
|
利润 |
|
|
|
(1)求利润![]() 关于月份
关于月份![]() 的线性回归方程;
的线性回归方程;
(2)试用(1)中求得的回归方程预测![]() 月和
月和![]() 月的利润;
月的利润;
(3)试用(1)中求得的回归方程预测该公司2016年从几月份开始利润超过![]() 万?
万?
相关公式: 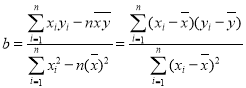 ,
, ![]() .
.
