题目内容
14.设函数f(x)=lnx+$\frac{a}{x-1}$(a为常数)(Ⅰ)若曲线y=f(x)在点(2,f(2))处的切线与x轴平行,求实数a的值;
(Ⅱ)若函数f(x)在(e,+∞)内有极值.求实数a的取值范围;
(Ⅲ)在(Ⅱ)的条件下,若x1∈(0,1),x2∈(1,+∞).求证:f(x2)-f(x1)>e+2-$\frac{1}{e}$(注:e是自然对数的底数).
分析 (Ⅰ)确定函数的定义域,求导数,利用曲线y=f(x)在点(2,f(2))处的切线与x轴平行,即可求实数a的值;
(Ⅱ)若函数f(x)在(e,+∞)内有极值,f′(x)=0在(e,+∞)内有不等的实根,令φ(x)=x2-(2+a)x+1=(x-α)(x-β),可得αβ=1,β>e.即可求实数a的取值范围;
(Ⅲ)确定函数f(x)在(0,α),(β,+∞)上单调递增,在(α,1),(1,β)上单调递减,可得f(x2)-f(x1)≥f(β)-f(α),再构造函数,即可证明结论.
解答 (Ⅰ)解:函数f(x)的定义域为(0,1)∪(1,+∞),
由f(x)=lnx+$\frac{a}{x-1}$得f′(x)=$\frac{1}{x}$-$\frac{a}{(x-1)^{2}}$,
∵曲线y=f(x)在点(2,f(2))处的切线与x轴平行,
∴f′(2)=0,
∴$\frac{1}{2}$-a=0,
∴a=$\frac{1}{2}$;
(Ⅱ)解:∵f′(x)=$\frac{{x}^{2}-(2+a)x+1}{x(x-1)^{2}}$,函数f(x)在(e,+∞)内有极值,
∴f′(x)=0在(e,+∞)内有不等的实根,
令φ(x)=x2-(2+a)x+1=(x-α)(x-β),可得αβ=1.
不妨设β>α,则α∈(0,1),β∈(1,+∞),
∴β>e.
∴φ(0)=1>0,
∴φ(e)=e2-(2+a)e+1<0,
∴a>e+$\frac{1}{e}$-2,
即实数a的取值范围是(e+$\frac{1}{e}$-2,+∞);
(Ⅲ)证明:由上知,f′(x)>0,可得0<x<α或x>β;f′(x)<0,可得α<x<1或1<x<β,
∴函数f(x)在(0,α),(β,+∞)上单调递增,在(α,1),(1,β)上单调递减,
由x1∈(0,1),得f(x1)≤f(α)=lnα+$\frac{α}{α-1}$,
x2∈(1,+∞),得f(x2)≥f(β)=lnβ+$\frac{β}{β-1}$,
∴f(x2)-f(x1)≥f(β)-f(α)
又αβ=1,α+β=a+2,β>e
∴f(β)-f(α)=lnβ+$\frac{β}{β-1}$-(lnα+$\frac{α}{α-1}$)=2lnβ+β-$\frac{1}{β}$,
令H(β)=2lnβ+β-$\frac{1}{β}$(β>e),
则H′(β)=($\frac{1}{β}$+1)2>0,
∴H(β)在(e,+∞)上单调递增,
∴H(β)>H(e)=e+2-$\frac{1}{e}$,
∴f(x2)-f(x1)>e+2-$\frac{1}{e}$.
点评 本题考查导数知识的综合运用,考查导数的几何意义,考查不等式的证明,考查函数的单调性,正确求导,确定函数的单调性是关键.

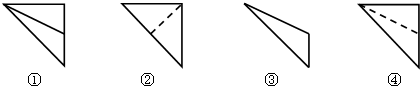
则该四面体的正视图和俯视图分别为( )
| A. | ①和③ | B. | ②和① | C. | ②和④ | D. | ④和③ |
| A. | S2012=-2012,a2012>a7 | B. | S2012=2012,a2012>a7 | ||
| C. | S2012=-2012,a2012<a7 | D. | S2012=2012,a2012<a7 |
 (
(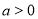 ,
,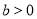 )经过点
)经过点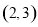 ,且离心率为
,且离心率为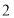 ,则它的焦距为( )
,则它的焦距为( ) B.
B.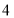
 D.
D.
 ,设
,设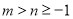 ,且
,且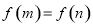 ,则
,则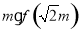 的最小值为( )
的最小值为( ) D.
D.