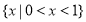题目内容
18.已知向量$\overrightarrow{a}$⊥$\overrightarrow{b}$,|$\overrightarrow{a}$-$\overrightarrow{b}$|=2,定义:cλ=λ$\overrightarrow{a}$+(1-λ)$\overrightarrow{b}$,其中0≤λ≤1.若${c_λ}•{c_{\frac{1}{2}}}=\frac{1}{2}$,则|cλ|的值不可能为( )| A. | $\frac{{\sqrt{5}}}{5}$ | B. | $\frac{{\sqrt{3}}}{3}$ | C. | $\frac{{\sqrt{2}}}{2}$ | D. | 1 |
分析 由题意可得$|\overrightarrow{{c}_{\frac{1}{2}}}|=1$,设$\overrightarrow{AB}=\overrightarrow{a},\overrightarrow{AC}=\overrightarrow{b},\overrightarrow{AD}=\overrightarrow{{c}_{\frac{1}{2}}},\overrightarrow{AP}=\overrightarrow{{c}_{λ}}$,则B,C,D,P四点共线,在圆中画出图形,由${c_λ}•{c_{\frac{1}{2}}}=\frac{1}{2}$得到两向量夹角的范围,从而求得|cλ|的范围得答案.
解答 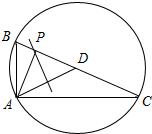 解:∵向量$\overrightarrow{a}$⊥$\overrightarrow{b}$,|$\overrightarrow{a}$-$\overrightarrow{b}$|=2,∴以$\overrightarrow{a},\overrightarrow{b}$为邻边的平行四边形为长方形,
解:∵向量$\overrightarrow{a}$⊥$\overrightarrow{b}$,|$\overrightarrow{a}$-$\overrightarrow{b}$|=2,∴以$\overrightarrow{a},\overrightarrow{b}$为邻边的平行四边形为长方形,
则$|\overrightarrow{a}+\overrightarrow{b}|=|\overrightarrow{a}-\overrightarrow{b}|=2$,
又$\overrightarrow{{c}_{λ}}$=λ$\overrightarrow{a}$+(1-λ)$\overrightarrow{b}$,∴$\overrightarrow{{c}_{\frac{1}{2}}}=\frac{1}{2}\overrightarrow{a}+\frac{1}{2}\overrightarrow{b}=\frac{1}{2}(\overrightarrow{a}+\overrightarrow{b})$,
则$|\overrightarrow{{c}_{\frac{1}{2}}}|=|\frac{1}{2}(\overrightarrow{a}+\overrightarrow{b})|=\frac{1}{2}$$|\overrightarrow{a}+\overrightarrow{b}|$=1.
设$\overrightarrow{AB}=\overrightarrow{a},\overrightarrow{AC}=\overrightarrow{b},\overrightarrow{AD}=\overrightarrow{{c}_{\frac{1}{2}}},\overrightarrow{AP}=\overrightarrow{{c}_{λ}}$,
由$\overrightarrow{{c}_{λ}}$=λ$\overrightarrow{a}$+(1-λ)$\overrightarrow{b}$,0≤λ≤1,可知B,C,D,P四点共线,
如右图,
设$<\overrightarrow{{c}_{\frac{1}{2}}},\overrightarrow{{c}_{λ}}>=θ$,
∵${c_λ}•{c_{\frac{1}{2}}}=\frac{1}{2}$,∴由$\frac{1}{2}=\overrightarrow{{c}_{λ}}•\overrightarrow{{c}_{\frac{1}{2}}}$=$|\overrightarrow{{c}_{λ}}|cosθ$,得$\overrightarrow{{c}_{λ}}$在$\overrightarrow{{c}_{\frac{1}{2}}}$上的投影为$\frac{1}{2}$,
∴当B、P两点重合时,$|\overrightarrow{{c}_{λ}}|=|\overrightarrow{{c}_{\frac{1}{2}}}|$=1,$θ=\frac{π}{3}$,
当P、D重合时,θ=0.
∴$|\overrightarrow{{c}_{λ}}|=\frac{1}{2cosθ}$,θ∈(0,$\frac{π}{3}$],cosθ∈[$\frac{1}{2}$,1),
∴$|\overrightarrow{{c}_{λ}}|∈(\frac{1}{2},1]$.
则|cλ|的值不可能为$\frac{\sqrt{5}}{5}$.
故选:A.
点评 本题考查平面向量的几何意义,涉及到向量的加、减法运算法则,三点共线的向量表示,向量的投影等知识,注意解题方法的积累,属于难题.

 一线名师权威作业本系列答案
一线名师权威作业本系列答案| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{3}{4}$ | D. | 1 |
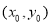 是直线
是直线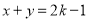 与圆
与圆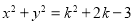 的公共点,则
的公共点,则 的取值范围是__________.
的取值范围是__________.
 点P是在平面直角坐标系中不在x轴上的一个动点,满足:过点P可作抛物线x2=y的两条切线,切点分别为A,B.
点P是在平面直角坐标系中不在x轴上的一个动点,满足:过点P可作抛物线x2=y的两条切线,切点分别为A,B.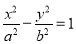 (
(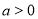 ,
,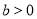 )经过点
)经过点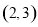 ,且离心率为
,且离心率为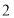 ,则它的焦距为( )
,则它的焦距为( ) B.
B.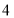
 D.
D.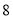
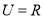 ,
,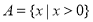 ,
,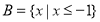 ,则集合
,则集合 ( )
( )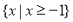 B.
B.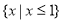
 D.
D.