题目内容
9.函数y=$\frac{{{x^2}+3}}{{\sqrt{{x^2}+2}}}$的最小值是$\frac{3\sqrt{2}}{2}$.分析 将函数化为y=($\frac{1}{2}$$\sqrt{{x}^{2}+2}$+$\frac{1}{\sqrt{{x}^{2}+2}}$)+$\frac{1}{2}$$\sqrt{{x}^{2}+2}$,注意运用基本不等式和二次函数的最值,同时注意最小值取得时,x的取值要一致,即可得到所求最小值.
解答 解:函数y=$\frac{{{x^2}+3}}{{\sqrt{{x^2}+2}}}$=$\frac{{x}^{2}+2+1}{\sqrt{{x}^{2}+2}}$
=$\sqrt{{x}^{2}+2}$+$\frac{1}{\sqrt{{x}^{2}+2}}$
=($\frac{1}{2}$$\sqrt{{x}^{2}+2}$+$\frac{1}{\sqrt{{x}^{2}+2}}$)+$\frac{1}{2}$$\sqrt{{x}^{2}+2}$
≥2$\sqrt{\frac{1}{2}}$+$\frac{1}{2}\sqrt{2}$=$\frac{3\sqrt{2}}{2}$.
当且仅当$\frac{1}{2}$$\sqrt{{x}^{2}+2}$=$\frac{1}{\sqrt{{x}^{2}+2}}$,即有x=0,取得等号.
则函数的最小值为$\frac{{3\sqrt{2}}}{2}$.
故答案为:$\frac{3\sqrt{2}}{2}$.
点评 本题考查基本不等式的运用:求最值,注意求最值的条件:一正二定三等,属于中档题和易错题.

练习册系列答案
相关题目
17.设数列{an}的前n项和Sn=$\frac{n(n+1)}{2}$,则a5=( )
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
14.随机变量ξ服从正态分布N(40,σ2),若P(ξ<30)=0.2,则P(30<ξ<50)=( )
| A. | 0.2 | B. | 0.4 | C. | 0.6 | D. | 0.8 |
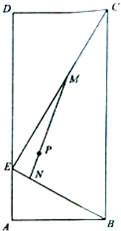 某生态农庄池塘的平面图为矩形ABCD,已知AB=4,BC=10,E为AD上一点,且AE=2,P为池塘内一临时停靠点,且P到AB,BC的距离均为3,EC,EB为池塘上浮桥,为了固定浮桥,现准备进过临时停靠点P再架设一座浮桥MN,其中M,N分别是浮桥EC,EB上点.(浮桥宽度、池塘岸边宽度不计),设EM=d,
某生态农庄池塘的平面图为矩形ABCD,已知AB=4,BC=10,E为AD上一点,且AE=2,P为池塘内一临时停靠点,且P到AB,BC的距离均为3,EC,EB为池塘上浮桥,为了固定浮桥,现准备进过临时停靠点P再架设一座浮桥MN,其中M,N分别是浮桥EC,EB上点.(浮桥宽度、池塘岸边宽度不计),设EM=d,