Question

【题目】设实数x，y满足 ，则z=|x﹣1|+|y+2|的取值范围为 ．

Answer 1

【答案】[2，6]
【解析】解：由约束条件 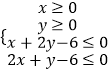作出可行域如图，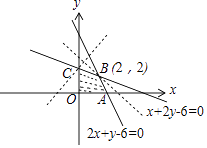

当x≥1，y≥0时，目标函数化为z=x+y+1，即y=﹣x+z﹣1，
∴当直线y=﹣x+z﹣1过（1，0）时，直线在y轴上的截距最小，z有最小值为2，当直线y=﹣x+z﹣1过（2，2）时，直线在y轴上的截距最大，z有最小值为5；
当0≤x＜1，y≥0时，目标函数化为z=﹣x+y+3，即y=x+z﹣3，
当直线y=x+z﹣3过（1，0）时，直线在y轴上的截距最小，∴z＞2，当直线y=x+z﹣3过（0，3）时，直线在y轴上的截距最大，z有最小值为6．
∴z=|x﹣1|+|y+2|的取值范围为[2，6]．
所以答案是：[2，6]．