题目内容
设
、
分别为不等边
的重心与外心
、
且
平行于
轴
(1)求
点的轨迹
的方程
(2)是否存在直线
过点
并与曲线交于
、
两点
且以
为直径的
圆过坐标原点
若存在求出直线的方程若不存在请说明理由
、分别为不等边的重心与外心、且平行于 轴
(1)求
点的轨迹的方程(2)是否存在直线
过点并与曲线交于、两点且以为直径的圆过坐标原点
若存在求出直线的方程若不存在请说明理由解：(1) 
即点的轨迹的方程
(2)存在直线
使得以为直径的圆过原点
即点的轨迹的方程(2)存在直线
使得以为直径的圆过原点本试题主要是考查了了轨迹方程的求解，以及直线与椭圆 位置关系的综合运用。
（1）设
则
显然
又设外心
由
得
解得
然后结合题目中的线线平行得到结论。
（2）假设存在直线满足题设条件
的方程为
代入
得
结合韦达定理和判别式，和向量的垂直问题，得到参数k的值。
（1）设
则显然又设外心
由得解得然后结合题目中的线线平行得到结论。（2）假设存在直线
满足题设条件的方程为代入得结合韦达定理和判别式，和向量的垂直问题，得到参数k的值。
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
：
，是否存在斜率为
的直线
,使
为直径的圆经过原点，若存在，求出直线
上，则点（m，c）不满足下列哪个方程（ ）
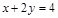
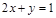
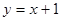上的一点向圆
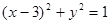引切线,则切线长的最小值为( )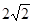
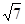
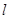把圆
的面积平分
则它被这个圆截得的弦长为( )
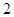
，直线L：
，直线L与圆C总有两个交点；
，求直线L的倾斜角；
,求此时直线L的方程.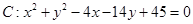
及点
.
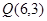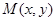为圆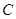
上任一点，求
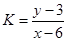的最大值和最小值；
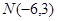，直线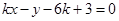
与圆C交于点A、B.当
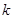为何值时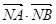
取到最小值。
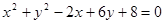的圆心和半径分别是
，2
2